[TOC]

基础算法

进制转化

int get(string s, int b)  // 将b进制的数转化成十进制
{
    int res = 0;
    // 秦九韶算法
    for (auto c: s)
        res = res * b + c - '0';
    return res;
}

排序

快速排序

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int i = l - 1, j = r + 1, x = q[ l + r >> 1];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

归并排序

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];

    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

二分

整数二分

bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}

浮点数二分

bool check(double x) {/* ... */} // 检查x是否满足某种性质
double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，一般题目要求是1e-6时，eps是1e-8
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

前缀和与差分

一维前缀和

#include <iostream>
using namespace std;
const int N = 100060;
int n, m, l, r, a[N], b[N];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        b[i] = b[i - 1] + a[i];
    }
    while (m--) {
        cin >> l >> r;
        cout << b[r] - b[l - 1] << endl;
    }
}

二维前缀和

#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int a[N][N], b[N][N];
int n, m, q;
int main() 
{
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> a[i][j];
            b[i][j] = b[i][j - 1] + b[i - 1][j] - b[i - 1][j - 1] + a[i][j];
        }
    }
    while (q--) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        cout << b[x2][y2] - b[x2][y1 - 1] - b[x1 - 1][y2] + b[x1 - 1][y1 - 1] << endl;
    }
}

一维差分

#include <iostream>
using namespace std;
const int N = 100010;
int n, m, a[N], b[N];
int main() 
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        b[i] = a[i] - a[i - 1];
    }
    while (m--) {
        int l, r, x;
        cin >> l >> r >> x;
        b[l] += x, b[r + 1] -= x;
    }
    for (int i = 1; i <= n; i++) {
        a[i] = a[i - 1] + b[i];
    }
    for (int i = 1; i <= n; i++) {
        cout << a[i] << " ";
    }
}

二维差分

/*
a[][]是差分矩阵，对差分矩阵求前缀和就得到了原数组，这和一维是完全一样的
不同于一维差分的是，二维差分进行修改区间需要修改四个点
a[x1][y1]+=d;进行求前缀和的时候，这会让所有x1,y1之后求的点都改变
所以要进行三个操作抵消
a[x2+1][y1]-=d,a[x1][y2+1]-=d,a[x2+1][y2+1]+=d;
insert函数便诞生了
最终的数组对差分数组求二维前缀和就行
*/
#include <bits/stdc++.h>
const int N = 1005;
using namespace std;
int n, m, q;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int d) {
    a[x1][y1] += d;
    a[x2 + 1][y1] -= d;
    a[x1][y2 + 1] -= d;
    a[x2 + 1][y2 + 1] += d;
}
int main() 
{
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            int x;
            cin >> x;
            insert(i, j, i, j, x);//可以看成在一个小区间进行insert
        }
    }
    while (q--) {
        int x1, y1, x2, y2, d;
        cin >> x1 >> y1 >> x2 >> y2 >> d;
        insert(x1, y1, x2, y2, d);
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            b[i][j] = b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1] + a[i][j];//二维前缀和
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cout << b[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

高精度

加法

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6;
vector<int> add(vector<int> A, vector<int> B) {
    vector<int> C;
    int t = 0;//进位
    for (int i = 0; i < A.size() || i < B.size(); i++) {
        if (i < A.size()) t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if (t) C.push_back(t);
    return C;
}
int main() 
{
    string a, b;
    cin >> a >> b;
    vector<int> A, B;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
    vector<int> C = add(A, B);
    for (int i = C.size() - 1; i >= 0; i--) cout << C[i];
    return 0;
}

减法

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6;
bool cmp(vector<int> a, vector<int> b)//比较大小
{
    if (a.size() != b.size()) return a.size() > b.size();
    for (int i = a.size() - 1; i >= 0; i--) {
        if (a[i] != b[i]) return a[i] > b[i];
    }
    return true;
}
vector<int> sub(vector<int> a, vector<int> b) {
    vector<int> c;
    int t = 0;//借位1
    for (int i = 0; i < a.size(); i++) {
        t = a[i] - t;
        if (i < b.size()) t -= b[i];
        c.push_back((t + 10) % 10);//有可能产生负数，这样就借1当10
        if (t < 0) t = 1;
        else t = 0;
    }
    while (c.size() > 1 && c.back() == 0) c.pop_back();//去除前导0
    return c;
}
int main() 
{
    vector<int> A, B, C;
    string a, b;
    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
    if (cmp(A, B)) C = sub(A, B);
    else {
        cout << "-";
        C = sub(B, A);
    }
    for (int i = C.size() - 1; i >= 0; i--) cout << C[i];
    return 0;
}

乘法

大数乘小数

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6;
vector<int> mul(vector<int> A, int b) {
    vector<int> c;
    int t = 0;//进位
    for (int i = 0; i < A.size(); i++) {
        t = A[i] * b + t;
        c.push_back(t % 10);
        t /= 10;
    }
    while (t) {
        c.push_back(t % 10);
        t /= 10;
    }
    while (c.size() > 1 && c.back() == 0) c.pop_back();
    return c;
}
int main() 
{
    string a;
    int b;
    cin >> a >> b;
    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    vector<int> c = mul(A, b);
    for (int i = c.size() - 1; i >= 0; i--) cout << c[i];
    return 0;
}

除法

大数除小数，先输出商，在输出余数

#include<bits/stdc++.h>
using namespace std;
vector<int> div(vector<int> &A, int B, int &r) {//r传入r的地址，便于直接对余数r进行修改
    vector<int> C;
    for (int i = 0; i < A.size(); i++) {//对A从最高位开始处理
        r = r * 10 + A[i];//将上次的余数*10在加上当前位的数字，便是该位需要除的被除数
        C.push_back(r / B);//所得即为商在这一位的数字
        r = r % B;
    }
    //由于在除法运算中，高位到低位运算，因此C的前导零都在vector的前面而不是尾部
    //vector只有删除最后一个数字pop_back是常数复杂度，而对于删除第一位没有相应
    //的库函数可以使用，而且删除第一位，其余位也要前移，
    //因此我们将C翻转，这样0就位于数组尾部，可以使用pop函数删除前导0
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}
int main() 
{
    string a;
    int B, r = 0; //代表余数
    cin >> a >> B;
    vector<int> A;
    for (int i = 0; i < a.size(); i++) A.push_back(a[i] - '0');//注意这次的A是由高为传输至低位，
    //由于在除法的手算过程中，发现从高位进行处理
    //for(int i=0;i<A.size();i++) cout<<A[i];
    //cout<<B;
    auto C = div(A, B, r);
    for (int i = C.size() - 1; i >= 0; i--) cout << C[i];//将C从最高位传给最低位
    cout << endl << r;//输出余数
    cout << endl;
    return 0;
}

离散化

离散化其实就是排序+去重，然后把值映射成[0,n-1]或者[1,n]，注意此时的n是去重后的n。

映射其实就是把值放入数组（vector）中，下标就是数组下标。

alls表示所有待离散化的数。

注意处理离散化问题的时候，往往需要先把所有用到的坐标存起来并且离散化，之后在进行各种操作。

#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
vector<PII> add, query;
vector<int> alls;
int a[300010], b[300010];//最多这么多下标
int find(int x) {
    int l = 0, r = alls.size() - 1;//因为就是存在vector里面
    while (l < r) {
        int mid = (l + r) >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return l + 1;
}
int main() 
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        int x, c;
        cin >> x >> c;
        add.push_back({x, c});
        alls.push_back(x);
    }
    for (int i = 1; i <= m; i++) {
        int l, r;
        cin >> l >> r;
        query.push_back({l, r});
        alls.push_back(l), alls.push_back(r);
    }
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());
    for (int i = 0; i < add.size(); i++) {
        int x = find(add[i].first), c = add[i].second;
        a[x] += c;
    }
    for (int i = 1; i <= alls.size(); i++) {
        b[i] = b[i - 1] + a[i];
    }
    for (int i = 0; i < query.size(); i++) {
        int l = find(query[i].first), r = find(query[i].second);
        cout << b[r] - b[l - 1] << endl;
    }
    return 0;
}

读入

string s;
getline(cin,s);//空格不断行输入
stringstream ss(s);
int x;//也可以改为string,double,char;
while(ss >> x) cout<<x<<endl;

//注意使用getline()之前，若使用了cin/scanf,必须要getchar()一次，过滤掉换行符，一次就行，多次getline()之间不需要getchar()
#include <bits/stdc++.h>
using namespace std;
int main() {
    int a;
    cin >> a;
    getchar();
    for (int i = 1; i <= 3; i++) {
        string s;
        getline(cin, s);
        cout << s << endl;
    }
    return 0;
}

//cin.get()不同于getline()应该在每次读入后都getchar()一次
#include <bits/stdc++.h>
using namespace std;
int main() {
    int a;
    cin >> a;
    getchar();
    for (int i = 1; i <= 3; i++) {
        char s[105];
        cin.get(s, 105);
        getchar();
        cout << s << endl;
    }
    return 0;
}

矩阵

#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define endl "\n"
typedef long long LL;
const int N = 1e5 + 10, M = N, mod = 1e9 + 7;
using namespace std;
struct Mat{
    int a[105][105];
    int r, c;
    Mat(int _r, int _c){
        r = _r, c = _c;
        memset(a, 0, sizeof a);
    }
    //单位矩阵
    void unit(){
        memset(a, 0, sizeof a);
        for(int i = 1; i <= r; i ++){
            a[i][i] = 1;
        }
    }
    Mat operator+(const Mat t) const{
        Mat ans = *this;
        for(int i = 1; i <= r; i ++){
            for(int j = 1; j <= c; j ++){
                ans.a[i][j] += t.a[i][j];
            }
        }
        return ans;
    }
    Mat operator-(const Mat t) const{
        Mat ans = *this;
        for(int i = 1; i <= r; i ++){
            for(int j = 1; j <= c; j ++){
                ans.a[i][j] -= t.a[i][j];
            }
        }
        return ans;
    }
    Mat operator*(const Mat t) const{
        Mat ans(r, t.c);
        int n = r, m = t.c;
        for(int i = 1; i <= n; i ++){
            for(int j = 1; j <= m; j ++){
                for(int k = 1; k <= c; k ++){
                    ans.a[i][j] += a[i][k] * t.a[k][j];
                    ans.a[i][j] %= mod;
                }
            }
        }
        return ans;
    }
    Mat pow(LL b){
        Mat ans(r, c), _a = *this;
        ans.unit();
        while(b){
            if(b & 1) ans = ans * _a;
            _a = _a * _a;
            b >>= 1;
        }
        return ans;
    }
    void output(){
        for(int i = 1; i <= r; i ++){
            for(int j = 1; j <= c; j ++){
                cout << a[i][j] << " ";
            }
            cout << endl;
        }
    }
};
int main()
{
    int n1, m1, n2, m2;
    cin >> m1 >> n1 >> m2 >> n2;
    Mat A(n1, m1), B(n2, m2);
    for(int i = 1; i <= n1; i ++){
        for(int j = 1; j <= m1; j ++){
            cin >> A.a[i][j];
        }
    }
    for(int i = 1; i <= n2; i ++){
        for(int j = 1; j <= m2; j ++){
            cin >> B.a[i][j];
        }
    }
    Mat ans = A * B;
    ans.output();
    return 0;
}

STL

Set/multiset

set和multiset会根据特定的排序原则将元素排序。两者不同之处在于，multisets允许元素重复，而set不允许重复。

s.insert() //log(n)
s.erase() //log(n)
s.begin() //返回第一个元素的地址
s.end() //返回最后一个元素下一个元素的地址
s.find(x) //log(n) 返回一个地址（迭代器），如果找不到当前元素x返回s.end()
s.lower_bound(x)// log(n) 返回一个元素>=x的地址（迭代器），如果找不到当前元素x返回s.end()
s.upper_bound(x)// log(n) 返回一个元素>x的地址（迭代器），如果找不到当前元素x返回s.end()

二分函数

lower_bound(首地址,尾地址,x)  //左闭右开，查找>=x的第一个数，若查找不到，返回尾地址
upper_bound(首地址,尾地址,x)  //左闭右开，查找>x的第一个数 ，若查找不到，返回尾地址 
//注意此函数返回的是地址，若要变成下标，若是数组a只需要-a,若是vector只需要-v.begin()

数据结构

字符串哈希

不能把字符映射成0，否则$A,AA,AAA$都是一样的。经验值$P=131$，或者$P=13331$，Q取成$2^{64}$,这样冲突的可能性很小。

/* 
全称字符串前缀哈希法，把字符串变成一个p进制数字（哈希值），实现不同的字符串映射到不同的数字。
对形如 X1X2X3⋯Xn−1XnX1X2X3⋯Xn−1Xn 的字符串,采用字符的ascii 码乘上 P 的次方来计算哈希值。
映射公式 (X1×Pn−1+X2×Pn−2+⋯+Xn−1×P1+Xn×P0)modQ  Q一般qu公式 (X1×Pn−1+X2×Pn−2+⋯+Xn−1×P1+Xn×P0)modQ  Q一般
注意
1. 任意字符不可以映射成0，否则会出现不同的字符串都映射成0的情况，比如A,AA,AAA皆为0
2. 冲突问题：通过巧妙设置P (131 或 13331) , Q (2的64次方)的值，一般可以理解为不产生冲突。

公式：前缀hash  h[i]=h[i-1]*P+str[i];
      区间hash  h[l,r]=h[r]−h[l−1]×P(r−l+1)次方
*/
#include <bits/stdc++.h>
typedef unsigned long long ULL;//代替对2的64次方取模
const int N = 1e6, P = 131;//P一般取131或者13331，
using namespace std;
ULL h[N], p[N];//h放的是前缀hash值，p放的是P的多少次方；
int l1, r1, l2, r2, n, m;
char str[N];
ULL query(int l, int r)//类似于前缀和，只不过需要一个偏移量
{
    return h[r] - h[l - 1] * p[r - l + 1];//公式
}
int main() 
{
    scanf("%d%d%s", &n, &m, str + 1);//注意s从数组的第一位开始存，类似于前缀和
    h[0] = 0, p[0] = 1;//初始化，P的0次方为1
    for (int i = 1; i <= n; i++) {
        h[i] = h[i - 1] * P + str[i];//计算前缀哈希，类似P进制,只要保证str[i]不是0就行
        p[i] = P * p[i - 1];//计算p的i次方，因为会用到一个P的(r−l+1)次方
    }
    while (m--) {
        scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
        if (query(l1, r1) == query(l2, r2)) printf("Yes\n");
        else printf("No\n");
    }
}

KMP

复杂度：$O(n)$

$p$是模板串，长度为$m$，$s$是要匹配的串，长度为$n$

$next[j]$的含义，以$p[j]$为结尾，最大的后缀和前缀相等的长度，当然长度要小于$j$，否则肯定是$k$

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int ne[N], n, m;
char s[N], p[N];
int main() {
    cin >> m >> (p + 1) >> n >> (s + 1);
    ne[0] = ne[1] = 0;
    for (int i = 2, j = 0; i <= m; i++)//和自己匹配
    {
        while (j && p[i] != p[j + 1]) j = ne[j]; 
        if (p[i] == p[j + 1]) j++;
        ne[i] = j;
    }
    for (int i = 1, j = 0; i <= n; i++)//匹配
    {
        while (j && s[i] != p[j + 1]) j = ne[j];//我们是用s[i]和p[j+1]比较，不相等就回退
        if (s[i] == p[j + 1]) j++;//如果相等，则i++，j++进行下一次匹配
        if (j == m)//匹配完成,不完成的话就匹配p[j+1]了
        {
            cout << i - m << " ";
            j = ne[j];//不要忘了
        }
    }
    return 0;
}

单调栈和队列

给定一个长度为 N 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1。

#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<int,int>PII;
const int N=1e6;
stack <int> stk;
int main()
{
    CLOSE;
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        int x;
        cin>>x;
        while(!stk.empty()&&stk.top()>=x) stk.pop();//当前这个点一定不会被用到，因为x更优
        if(!stk.empty()) cout<<stk.top()<<" ";
        else cout<<-1<<" ";
        stk.push(x);
    }
    return 0;
}

单调队列

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6;
deque<int> q;//双端队列
int a[N];
int main() {
    int n, k;
    cin >> n >> k;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) {
        while (!q.empty() && a[q.back()] >= a[i]) q.pop_back();//制作队列
        q.push_back(i);
        while (!q.empty() && i - q.front() + 1 > k) q.pop_front();//因为要求长度是k
        if (i >= k) cout << a[q.front()] << " ";
    }
    cout << endl;
    q.clear();//别忘了
    for (int i = 1; i <= n; i++) {
        while (!q.empty() && a[q.back()] <= a[i]) q.pop_back();
        q.push_back(i);
        while (!q.empty() && i - q.front() + 1 > k) q.pop_front();
        if (i >= k) cout << a[q.front()] << " ";
    }
    return 0;
}

并查集

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6;
int p[N], siz[N];
int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}
int merge(int x, int y) {
    int fx = find(x);
    int fy = find(y);
    if (fx != fy) {
        p[fx] = fy;
        siz[fy] += siz[fx];
    }
}
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        p[i] = i;
        siz[i] = 1;
    }
    while (m--) {
        string op;
        int a, b;
        cin >> op;
        if (op == "C") {
            cin >> a >> b;
            merge(a, b);
        } else if (op == "Q1") {
            cin >> a >> b;
            if (find(a) == find(b)) cout << "Yes" << "\n";
            else cout << "No" << "\n";
        } else {
            cin >> a;
            cout << siz[find(a)] << "\n";
        }
    }
    return 0;
}

DFS序

树上单点修改，子树求和问题。

dfs把子树转换成区间，子树对应的区间一定是连续的。

#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define endl "\n"
typedef long long LL;
const int N = 1e6 + 10, M = 2 * N, mod = 1e9 + 7;
using namespace std;
int n, m, k, a[N], t[N];
int h[N], e[M], ne[M], idx;
int l[N], r[N], timestamp;
void add(int x, int y){
    e[idx] = y, ne[idx] = h[x], h[x] = idx ++;
}
int lowbit(int x){return x & -x;}
void addT(int x, int c){
    for(int i = x; i <= n; i += lowbit(i)){
        t[i] += c;
    }
}
LL getSum(int x){
    LL ans = 0;
    for(int i = x; i; i -= lowbit(i)){
        ans += t[i];
    }
    return ans;
}
//u子树对应的区间就是l[u],r[u]
void dfs(int u, int fa){
    l[u] = ++ timestamp;
    for(int i = h[u]; ~ i; i = ne[i]){
        int j = e[i];
        if(j == fa) continue;
        dfs(j, u);
    }
    r[u] = timestamp;
}
int main()
{
    CLOSE;
    cin >> n >> m >> k;
    memset(h, -1, sizeof h);
    for(int i = 1; i <= n; i ++) cin >> a[i];
    for(int i = 1; i < n; i ++){
        int x, y;
        cin >> x >> y;
        add(x, y), add(y, x);
    }
    dfs(k, -1);
    for(int i = 1; i <= n; i ++){
        addT(l[i], a[i]);
    }
    while(m --){
        int op, x, y;
        cin >> op >> x;
        if(op == 1){
            cin >> y;
            addT(l[x], y);
        } else{
            cout << getSum(r[x]) - getSum(l[x] - 1) << endl;
        }
    }
    return 0;
}

ST表

#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define endl "\n"
typedef long long LL;
const int N = 2e5 + 10, M = 19, mod = 1e9 + 7;
using namespace std;
int f[N][M], a[N];
void init(int n){
    int x = log2(n);
    for(int j = 0; j <= x; j ++){
        for(int i = 1; i + (1 << j) - 1 <= n; i ++){
            if(!j) f[i][j] = a[i];
            else f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
        }
    }
}
int query(int l, int r){
    int k = log2(r - l + 1);
    return max(f[l][k], f[r - (1 << k) + 1][k]);
}
int main()
{
    int n, m;
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    init(n);
    cin >> m;
    while(m --){
        int l, r;
        cin >> l >> r;
        cout << query(l, r) << endl;
    }
    return 0;
}

树状数组

单点修改，区间求和

#include <bits/stdc++.h>
typedef long long LL;
const int N = 5e5 + 10, M = N;
using namespace std;
int a[N], n, m;
LL t[N];
int lowbit(int x){return x & -x;}
void add(int x, int c){
    for(int i = x; i <= n; i += lowbit(i)){
        t[i] += c;
    }
}
LL query(int x){
    LL sum = 0;
    for(int i = x; i; i -= lowbit(i)){
        sum += t[i];
    }
    return sum;
}
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++){
        cin >> a[i];
        add(i, a[i]);
    }
    while(m --){
        int op, x, y;
        cin >> op >> x >> y;
        if(op == 1) add(x, y);
        else cout << query(y) - query(x - 1) << endl;
    }
    return 0;
}

区间修改，单点查询，即维护差分数组

#include <bits/stdc++.h>
typedef long long LL;
const int N = 5e5 + 10, M = N;
using namespace std;
int a[N], n, m;
LL t[N];
int lowbit(int x){return x & -x;}
void add(int x, int c){
    for(int i = x; i <= n; i += lowbit(i)){
        t[i] += c;
    }
}
LL query(int x){
    LL sum = 0;
    for(int i = x; i; i -= lowbit(i)){
        sum += t[i];
    }
    return sum;
}
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++){
        cin >> a[i];
        add(i, a[i] - a[i - 1]);
    }
    while(m --){
        int op;
        cin >> op;
        if(op == 1) {
            int l, r, k;
            cin >> l >> r >> k;
            add(l, k), add(r + 1, -k);
        }
        else {
            int x;
            cin >> x;
            cout << query(x) << endl;
        }
    }
    return 0;
}

#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define endl "\n"
typedef long long LL;
const int N = 1e6 + 10, M = N, mod = 1e9 + 7;
using namespace std;
int n, q;
LL  t1[N], t2[N], a[N], b[N];
int lowbit(int x) {return x & -x;}
void add(int x, LL c, LL t[]){
    for(int i = x; i <= n; i += lowbit(i)){
        t[i] += c;
    }
}
LL getsum(int x, LL t[]){
    LL sum = 0;
    for(int i = x; i; i -= lowbit(i)){
        sum += t[i];
    }
    return sum;
}
LL query(int x){
    return getsum(x, t1) * (x + 1) - getsum(x, t2); 
}
int main()
{
    CLOSE;
    cin >> n >> q;
    for(int i = 1; i <= n; i ++){
        cin >> a[i];
    }
    for(int i = 1; i <= n; i ++){
        b[i] = a[i] - a[i - 1];
        add(i, b[i], t1);
        add(i, b[i] * i, t2);
    }
    while(q --){
        int op;
        cin >> op;
        if(op == 1){
            int l, r;
            LL k;
            cin >> l >> r >> k;
            add(r + 1, -k, t1), add(l, k, t1);//改差分数组
            add(r + 1, -k * (r + 1), t2), add(l, k * l, t2);//改i*差分数组
        } else{
            int l, r;
            cin >> l >> r;
            cout << query(r) - query(l - 1) << endl;
        }
    }
    return 0;
}

线段树

建树复杂度 $O(n)$,其他操作$O(log(n))$

父节点：x/2 int会自动下取整 x>>1; 左儿子：2x x<<1; 右儿子：2x+1 x<<1|1

凡是只修改单点的，是不需要懒标记的，修改区间的需要懒标记。

pushup（）放在build和modify的下面

pushdown放在query和modify的上面，并且pushdown放在的是要分裂的地方；

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 100;
struct node {
    LL l, r, sum, add;
} t[N * 4];//开四倍空间
LL a[N];
void pushup(LL u)//用子节点的信息更新父亲节点
{
    t[u].sum = t[u << 1].sum + t[u << 1 | 1].sum;
};
void pushdown(LL u)//用父节点去更新子节点
{
    //更新的信息包括值和懒标记，不要忘了清空父节点的信息，这更像传递！！！
    t[u << 1].sum += (t[u << 1].r - t[u << 1].l + 1) * t[u].add;//更新左儿子的值
    t[u << 1 | 1].sum += (t[u << 1 | 1].r - t[u << 1 | 1].l + 1) * t[u].add;//更新右儿子的值
    t[u << 1].add += t[u].add;//更新左儿子的懒标记
    t[u << 1 | 1].add += t[u].add;//更新右儿子的值
    t[u].add = 0;//清空父节点的懒标记
}
void build(int u, int l, int r) {
    t[u].l = l, t[u].r = r;//这个一定不要忘了
    if (l == r)//初始化
    {
        t[u].sum = a[l];
        t[u].add = 0;
    } else {
        t[u].add = 0;//最好也加上
        int mid = (l + r) >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);//上面的代码修改了子节点，父节点的值必须更新
    }
}
void modify(int u, int l, int r, LL d)//l,r是要修改的区间
{
    if (l <= t[u].l && t[u].r <= r)//当前区间是修改区间的子区间
    {
        t[u].sum += (t[u].r - t[u].l + 1) * d;//直接修改当前区间，不在递归修改后面区间了
        t[u].add += d;//更新懒标记
    } else//修改部分区间的情况
    {
        pushdown(u);//要修改部分区间了，分裂了，要pushdown（）
        int mid = (t[u].r + t[u].l) >> 1;//这里一定不要错了，l,r是要修改的区间
        if (l <= mid) modify(u << 1, l, r, d);//左儿子有交集，递归修改左半边
        if (r > mid) modify(u << 1 | 1, l, r, d);//右儿子有交集，递归修改右半边
        pushup(u);//修改了子节点，必然要更新父节点
    }
}
LL query(int u, int l, int r) {
    if (l <= t[u].l && t[u].r <= r) {
        return t[u].sum;//直接返回
    } else//查询部分区间情况
    {
        pushdown(u);//查询的时候不要忘了pushdown()
        int mid = (t[u].l + t[u].r) >> 1;//不要用l,r, l,r是要查询的区间左右端点
        LL ans = 0;
        if (l <= mid) ans += query(u << 1, l, r);//左儿子有交集，递归查询左半边
        if (r > mid) ans += query(u << 1 | 1, l, r);//右儿子有交集，递归查询右半边
        return ans;
    }
}
int n, m;
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
    build(1, 1, n);
    while (m--) {
        char op;
        LL l, r, d;
        cin >> op >> l >> r;
        if (op == 'Q') {
            cout << query(1, l, r) << endl;
        } else {
            cin >> d;
            modify(1, l, r, d);
        }
    }
}

字典树

void insert(string s){
    int p = 0;
    for(int i = 0; i < s.size(); i ++){
        int u = s[i] - '0';
        if(!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p] ++;
}
int query(string s){
    int p = 0;
    for(int i = 0; i < s.size(); i ++){
        int u = s[i] - '0';
        if(!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

01字典树

cnt[p] ++，保证只用一次，用完了就不会跳到x！！

#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define endl "\n"
typedef long long LL;
const int N = 3e5 + 10, M = N, mod = 1e9 + 7;
using namespace std;
int son[N][2], cnt[N], idx;
int a[N];
void insert(int x){
    int p = 0;
    for(int i = 30; i >= 0; i --){
        int u = (x >> i) & 1;
        if(!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
        cnt[p] ++;
    }
}
int query(int x){
    int p = 0, ans = 0;
    for(int i = 30; i >= 0; i --){
        int u = (x >> i) & 1;
        if(cnt[son[p][u]]){
            p = son[p][u];
        } else {
            p = son[p][u ^ 1];
            ans += 1 << i;
        }
        cnt[p] --;
    }
    return ans;
}
int main()
{
    int n;
    cin >> n;
    for(int i = 1; i <= n; i ++){
        cin >> a[i];
    }
    for(int i = 1; i <= n; i ++){
        int x;
        cin >> x;
        insert(x);
    }
    for(int i = 1; i <= n; i ++){
        cout << query(a[i]) << " ";
    }
    return 0;
}

搜索

BFS

bfs中的队列有两个性质

1：两段性 距离： x x x x (x+1) (x+1) (x+1)

2：单调性 bfs每次取出的队头都是距离最近的点，类似于Dijisitla，

3：只要能时时刻刻满足两段性和单调性，呢么bfs就相当于Dijisitla，所以bfs是正确的；

双端队列广搜

1：双端队列广搜解决的问题是边权是0和边权是1的问题，普通的BFS是解决边权都是1（边权相等）的问题；

2：双端队列可以说是简化版的堆优化Dijisitla，但是复杂度更优为O(n)；

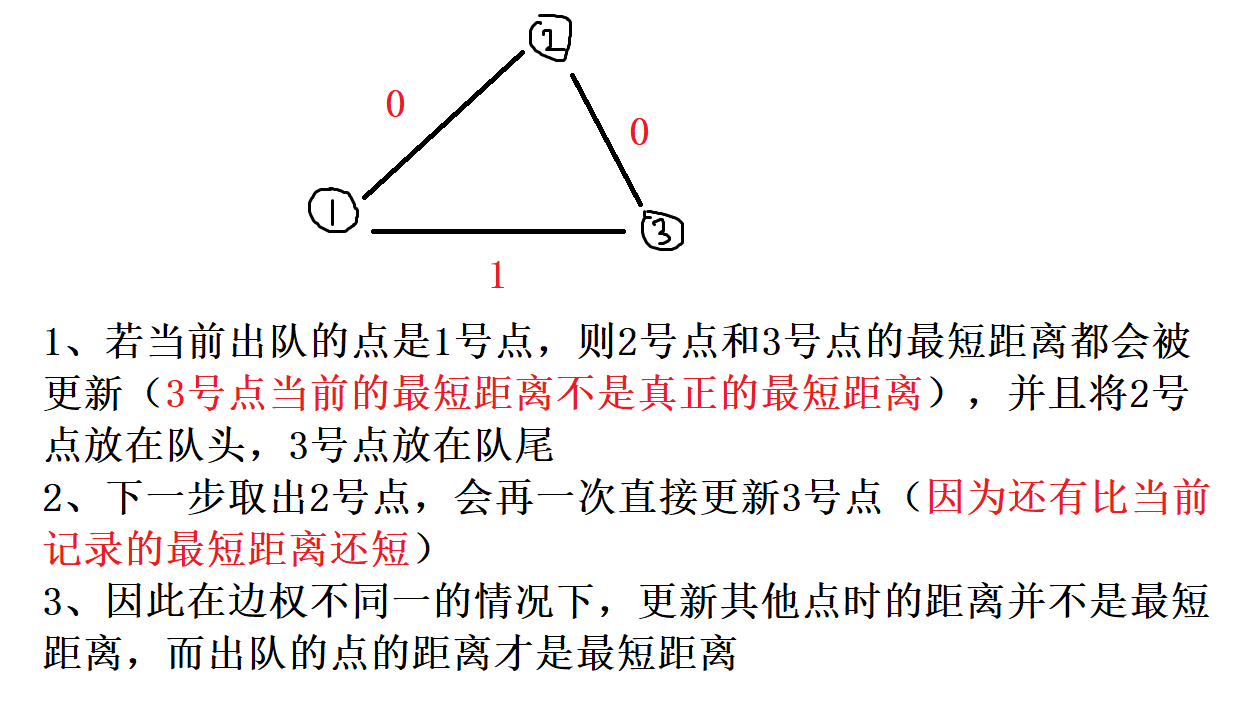
3：因为有两种权重，第一次搜到的点不一定就是最短距离，与堆优化Dijkstra 一样，必须在出队时才知道每个点最终的最小值，而和一般的bfs不一样，原因是如下图所示

4.与Dijisitla不同是，他是搜索的时候用，不需要建边，不需要建图，与普通的bfs题的不同是有两种边。

#include <bits/stdc++.h>

const int N = 1006;
using namespace std;
struct node {
    int x, y;
};
int a[N][N], dist[N][N], st[N][N];
int wy[4][2] = {1, 0},{-1, 0},{0, 1},{0,-1};
int qdx, qdy;
int bfs() {
    memset(dist, 0x3f, sizeof dist);
    deque<node> q;
    q.push_front({qdx, qdy});
    dist[qdx][qdy] = 0;
    while (!q.empty()) {
        node one = q.front();
        q.pop_front();
        if (st[one.x][one.y]) continue;
        else st[one.x][one.y] = 1;
        for (int i = 0; i <= 3; i++) {
            int xx = one.x + wy[i][0];
            int yy = one.y + wy[i][1];
            if (xx >= 0 && xx < N && yy >= 0 && yy <= N) {
                if (dist[xx][yy] > dist[one.x][one.y] + a[xx][yy]) {
                    dist[xx][yy] = dist[one.x][one.y] + a[xx][yy];
                    if (a[xx][yy] == 1)q.push_back({xx, yy});
                    else q.push_front({xx, yy});
                }
            }
        }
    }
    return dist[0][0];
}
int main() {
    int n;
    cin >> n >> qdx >> qdy;
    for (int i = 1; i <= n; i++) {
        int x, y;
        cin >> x >> y;
        a[x][y] = 1;
    }
    cout << bfs();
    return 0;
}

双向广搜

一般用于最小步数模型，最短路模型一般用不到，因为本来就不会超时，比如我们要看一个字符串十步之内是不是能变到另一个字符串，如果有六个变化方式，直接BFS是6^10,如果是双向广搜的话，只有3*6的五次方，显然是一个很大的优化，而不是简单的/2。

//字符串函数  s.substr(qd,len);
#include <bits/stdc++.h>
using namespace std;
string A, B, x, y;
string a[7], b[7];
unordered_map<string, int> da, db;
queue<string> qa, qb;
int idx = 0;
int extend(queue<string> &q, unordered_map<string, int> &da, unordered_map<string, int> &db, string a[],
           string b[])//别忘了加引用符号
{
    string s = q.front();
    q.pop();
    for (int i = 0; i < s.size(); i++)//遍历起点
    {
        for (int j = 1; j <= idx; j++)//遍历规则
        {
            if (s.substr(i, a[j].size()) == a[j])//函数
            {
                string ss = s.substr(0, i) + b[j] + s.substr(i + a[j].size());//变换后的字符串
                if (db.count(ss))//如果另一个遍历到了这个，就要汇合
                {
                    return da[s] + db[ss] + 1;//返回距离
                }
                if (da.count(ss)) continue;//如果a搜过了，就不入队了
                q.push(ss);
                da[ss] = da[s] + 1;
            }
        }
    }
    return 11;//搜素一层都没有返回，直接返回11
}
int bfs() {
    if (A == B) return 0;//特判
    da[A] = 0, db[B] = 0;
    qa.push(A), qb.push(B);
    while (!qa.empty() && !qb.empty())//如果有一个为空了，说明是不连通的，无法从A->B
    {
        int bs;
        if (qa.size() <= qb.size())//优化，优先搜索队列长度短的
        {
            bs = extend(qa, da, db, a, b);//进行一次扩展看看双向搜索是否能接在一起
        } else bs = extend(qb, db, da, b, a);//进行一次扩展看看双向搜索是否能接在一起
        if (bs <= 10) return bs;//如果距离小于10，就找到了，不用继续搜索了
    }
    return -1;//全部情况都搜索了，没有<10的，呢么无解
}
int main() {
    cin >> A >> B;
    while (cin >> x >> y) {
        idx++;
        a[idx] = x, b[idx] = y;
    }
    int ans = bfs();
    if (ans == -1) puts("NO ANSWER!");
    else cout << ans << endl;
    return 0;
}

图和树

二叉树

先序+中序

#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e3;
map<int, PII> node;
map<int, int> mp;
int n;
int a[N], b[N];
vector<int> v;
int dfs(int l1, int r1, int l2, int r2)//先序+中序
{
    if (l1 > r1 || l2 > r2) return 0;
    int root = a[l1];
    int k = mp[root];
    int sum = k - l2;
    node[root].first = dfs(l1 + 1, l1 + sum, l2, k - 1);
    node[root].second = dfs(l1 + sum + 1, r1, k + 1, r2);
    return root;
}
int dfs(int l1, int r1, int l2, int r2)//后序+中序
{
    if (l1 > r1 || l2 > r2) return 0;
    int root = a[r1];
    int k = mp[root];
    int sum = k - l2;
    node[root].first = dfs(l1, l1 + sum - 1, l2, k - 1);
    node[root].second = dfs(l1 + sum, r1 - 1, k + 1, r2);
    return root;
}
void bfs()//层次
{
    queue<int> q;
    q.push(a[1]);
    int cnt = 0;
    while (!q.empty()) {
        int t = q.front();
        q.pop();
        cnt++;
        if (cnt != n) cout << t << " ";
        else cout << t << endl;
        if (node[t].first) {
            q.push(node[t].first);
        }
        if (node[t].second) {
            q.push(node[t].second);
        }
    }
}
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> b[i];
        mp[b[i]] = i;
    }
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    dfs(1, n, 1, n);
    bfs();
    return 0;
}

树的直径和重心

直径

#include <bits/stdc++.h>
using namespace std;
const int N = 10010, M = 20010;
int h[N], ne[M], w[M], e[M], idx;
int ans; // 保存最长路径
int t;  // 保存找到的最远点
int n;
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u, int father, int dist) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        dfs(j, u, dist + w[i]);
    }
    // 找到最大的dist用来更新答案ans和点t
    if (dist > ans) {
        ans = dist;
        t = u;
    }
}
int main() {
    memset(h, -1, sizeof h);
    scanf("%d", &n);
    for (int i = 0; i < n - 1; ++i) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
        add(b, a, c);
    }
    dfs(1, -1, 0);  // 先找到点t
    dfs(t, -1, 0);  // 根据t找到结果ans
    printf("%d", ans);
    return 0;
}

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。树的重心不唯一。

定义函数$dfs(u)$，表示以$u$为根的子树的节点个数。

#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = N * 2;
int n;
int h[N], e[M], ne[M], idx;//存图
int ans = 0x3f3f3f3f;//最终的答案
bool st[N];//表示哪些点已经被遍历过
//加边函数
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
//dfs(u)返回的结果是以u为根的子树的节点个数
int dfs(int u) {
    st[u] = true;//u节点被访问过
    int size = 0;//size存的是若删除u节点，剩余各个连通块中点数的最大值的最小是多少。
    int sum = 1;// sum存的是以u为根的子树的节点个数，也就是dfs函数最后返回的值，初值是1
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];//j是子节点的编号
        if (st[j]) continue;//只访问没有访问过的点
        int s = dfs(j);//子树的节点个数
        size = max(size, s);//取一个max
        sum += s;//以u为根的子树的节点个数需要加上s
    }
    size = max(size, n - sum);//不要忘了父节点也构成了一个联通块
    ans = min(ans, size);//更新答案
    return sum;
}
int main() {
    scanf("%d", &n);
    memset(h, -1, sizeof h);//别忘了初始化图
    for (int i = 0; i < n - 1; i++) {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }
    dfs(1);//从任意一个点搜都可以
    printf("%d\n", ans);
    return 0;
}

拓扑排序

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 100, M = N;
int h[N], e[M], ne[M], idx, din[N], n, m;
vector<int> v;
void add(int x, int y) {
    e[idx] = y, ne[idx] = h[x], h[x] = idx++;
}
void topsort() {
    queue<int> q;
    for (int i = 1; i <= n; i++) {
        if (din[i] == 0) q.push(i);
    }
    while (!q.empty()) {
        int t = q.front();
        q.pop();
        v.push_back(t);
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            din[j]--;
            if (din[j] == 0) q.push(j);
        }
    }
}
int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int x, y;
        cin >> x >> y;
        add(x, y);
        din[y] ++;
    }
    topsort();
    if (v.size() != n) cout << -1;
    else {
        for (int i = 0; i < v.size(); i++) cout << v[i] << " ";
    }
    return 0;
}

最小生成树

Kruskal复杂度 $O(n*log(n))$

#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<int,int>PII;
const int N=1e5+100,M=2e5+100;
struct node{
    int x,y,w;
}edge[M];
bool cmp(node a,node b)
{
    return a.w<b.w;
}
int n,m,p[N];
int find(int x)
{
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}
int main()
{
    CLOSE;
    cin>>n>>m;
    for(int i=1;i<=n;i++) p[i]=i;
    for(int i=1;i<=m;i++)
    {
        cin>>edge[i].x>>edge[i].y>>edge[i].w;
    }
    sort(edge+1,edge+1+m,cmp);//这里排序别排错了
    int sum=0,cnt=0;
    for(int i=1;i<=m;i++)
    {
        int x=find(edge[i].x),y=find(edge[i].y),w=edge[i].w;
        if(x!=y)
        {
            cnt++;
            sum+=w;
            p[x]=y;
        }
    } 
    if(cnt==n-1) cout<<sum<<endl;
    else cout<<"impossible"<<endl;
    return 0;
}

次小生成树

严格次小生成树：边权之和必须小于最小生成树

非严格次小生成树，边权之和可以与最小生成树相等

//离谱，卡vector！！！
#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 1e5 + 10, M = 6e5 + 100, inf = 0x3f3f3f3f;
int h[N], e[M], ne[M], w[M], idx;
int f[N][18], depth[N], d1[N][18], d2[N][18], p[N];
int n, m;
ll sum;
void add(int x, int y, int z) {
    e[idx] = y, w[idx] = z, ne[idx] = h[x], h[x] = idx++;
}
int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}
struct node {
    int x, y, w;
    bool used;
} edge[M];
bool cmp(node a, node b) {
    return a.w < b.w;
}
void bfs() {
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0;
    depth[1] = 1;
    queue<int> q;
    q.push(1);
    while (!q.empty()) {
        int t = q.front();
        q.pop();
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (depth[j] > depth[t] + 1) {
                q.push(j);
                depth[j] = depth[t] + 1;
                f[j][0] = t;
                d1[j][0] = w[i], d2[j][0] = -inf;
                for (int k = 1; k <= 17; k++) {
                    int anc = f[j][k - 1];
                    f[j][k] = f[anc][k - 1];
                    int distance[4] = {d1[j][k - 1], d1[anc][k - 1], d2[j][k - 1], d2[anc][k - 1]};
                    d1[j][k] = d2[j][k] = -inf;
                    for (int s = 0; s <= 3; s++) {
                        if (distance[s] > d1[j][k]) {
                            d2[j][k] = d1[j][k], d1[j][k] = distance[s];
                        } else if (distance[s] < d1[j][k] && distance[s] > d2[j][k]) d2[j][k] = distance[s];
                    }
                }
            }
        }
    }
}
int lca(int x, int y, int w) {
    int distance[M];
    int cnt = 0;
    if (depth[x] < depth[y]) swap(x, y);
    for (int i = 17; i >= 0; i--) {
        if (depth[f[x][i]] >= depth[y]) {
            distance[cnt++] = d1[x][i];
            distance[cnt++] = d2[x][i];
            x = f[x][i];
        }
    }
    if (x != y) {
        for (int i = 17; i >= 0; i--) {
            if (f[x][i] != f[y][i]) {
                distance[cnt++] = d1[x][i];
                distance[cnt++] = d2[x][i];
                distance[cnt++] = d1[y][i];
                distance[cnt++] = d2[y][i];
                x = f[x][i], y = f[y][i];
            }
        }
        distance[cnt++] = d1[x][0];
        distance[cnt++] = d2[x][0];
        distance[cnt++] = d1[y][0];
        distance[cnt++] = d2[y][0];
    }
    int dist1 = -inf, dist2 = -inf;
    for (int i = 0; i < cnt; i++) {
        int it = distance[i];
        if (it > dist1) {
            dist2 = dist1, dist1 = it;
        } else if (it < dist1 && it > dist2) dist2 = it;
    }
    if (w > dist1) return w - dist1;
    else if (w > dist2) return w - dist2;
    else return inf;
}
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) p[i] = i;
    memset(h, -1, sizeof h);
    for (int i = 1; i <= m; i++) {
        int x, y, z;
        scanf("%d%d%d", &x, &y, &z);
        edge[i] = {x, y, z, false};
    }
    sort(edge + 1, edge + 1 + m, cmp);
    for (int i = 1; i <= m; i++) {
        int fx = find(edge[i].x), fy = find(edge[i].y), w = edge[i].w;
        if (fx != fy) {
            p[fx] = fy;
            sum += w;
            edge[i].used = true;
            add(edge[i].x, edge[i].y, w);
            add(edge[i].y, edge[i].x, w);
        }
    }
    bfs();
    ll ans = 1e18;
    for (int i = 1; i <= m; i++) {
        if (!edge[i].used) {
            int x = edge[i].x, y = edge[i].y;
            ans = min(ans, sum + lca(x, y, edge[i].w));
        }
    }
    printf("%lld\n", ans);
    return 0;
}

最短路

Dijkstra

只能正权

#include<bits/stdc++.h>
typedef long long LL;
const int N = 1e5 + 10, M = 2 * N;
using namespace std;
int h[N], e[M], ne[M], w[M], dist[N], idx;
bool st[N];
int n, m;
struct node{
    int x, dist;
};
struct cmp{
    bool operator()(node a, node b){
        return a.dist > b.dist;
    }
};
void add(int x, int y, int z){
    e[idx] = y, w[idx] = z, ne[idx] = h[x], h[x] = idx ++;
}
void dij(){
    priority_queue<node, vector<node>, cmp> q;
    q.push({1, 0});
    dist[1] = 0;
    while(!q.empty()){
        node t = q.top();
        q.pop();
        if(st[t.x]) continue;
        st[t.x] = true;
        for(int i = h[t.x]; ~ i; i = ne[i]){
            int j = e[i];
            if(dist[j] > dist[t.x] + w[i]){
                dist[j] = dist[t.x] + w[i];
                q.push({j, dist[j]});
            }
        }
    }
}
int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    memset(dist, 0x3f, sizeof dist);
    for(int i = 1; i <= m; i ++){
        int x, y, z;
        cin >> x >> y >> z;
        add(x, y, z);
    }
    dij();
    cout << (dist[n] > 0x3f3f3f3f / 2 ? -1 : dist[n]);
    return 0;    
}

朴素版

#include <bits/stdc++.h>
using namespace std;
const int N = 600;
int a[N][N], bj[N], s[N];
int n, m, x, y, z;
int f() {
    s[1] = 0;
    for (int i = 1; i <= n; i++) {
        int t = -1;
        for (int j = 1; j <= n; j++) {
            if (bj[j] == 0 && (t == -1 || s[j] < s[t])) {
                t = j;
            }
        }
        bj[t] = 1;
        for (int j = 1; j <= n; j++) {
            s[j] = min(s[j], s[t] + a[t][j]);
        }

    }
    if (s[n] > 0x3f3f3f3f / 2) return -1;
    else return s[n];
}
int main() {
    memset(a, 0x3f, sizeof a);
    memset(s, 0x3f, sizeof s);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        cin >> x >> y >> z;
        a[x][y] = min(a[x][y], z);
    }
    int t = f();
    cout << t;
}

Bellman-ford

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离，如果无法从 1 号点走到 n 号点，输出 impossible。

注意：图中可能存在负权回路 。

#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, M = 10010;
struct Edge{
    int a, b, c;
}edges[M];
int n, m, k, dist[N], last[N];
void bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for (int i = 0; i < k; i ++ ){
        memcpy(last, dist, sizeof dist);
        for (int j = 0; j < m; j ++ ){
            auto e = edges[j];
            dist[e.b] = min(dist[e.b], last[e.a] + e.c);
        }
    }
}
int main()
{
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 0; i < m; i ++ ){
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        edges[i] = {a, b, c};
    }
    bellman_ford();
    if (dist[n] > 0x3f3f3f3f / 2) puts("impossible");
    else printf("%d\n", dist[n]);
    return 0;
}

Spfa

负权可以

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 100, M = N;
int h[N], e[M], ne[M], w[M], idx, n, m, st[N], dist[N];
void add(int x, int y, int z) {
    e[idx] = y, w[idx] = z, ne[idx] = h[x], h[x] = idx++;
}
void spfa() {
    queue<int> q;
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    st[1] = 1;
    q.push(1);
    while (!q.empty()) {
        int t = q.front();
        q.pop();
        st[t] = 0;
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (dist[j] > dist[t] + w[i]) {
                dist[j] = dist[t] + w[i];
                if (!st[j]) {
                    st[j] = 1;
                    q.push(j);
                }
            }
        }
    }
}
int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int x, y, z;
        cin >> x >> y >> z;
        add(x, y, z);
    }
    spfa();
    if (dist[n] >= 0x3f3f3f3f / 2) cout << "impossible";
    else cout << dist[n];
    return 0;
}

Floyd

Floyd可以解决的问题：不含负环

1：最短路

floyd实际上是一种dp，d[k,i,j]表示从i出发到达j，只经过节点编号不超过k的最短路。

呢么可以分为两种，包含节点k和不包含节点k，因为没有负环，所以floyd算的的最短路中一定没有重复点，否则就有负环。

呢么d[k,i,j]=min(d[k-1,i,j],d[k-1,i,k]+d[k-1,k,j];发现可以去掉一维

d[i,j]=min(d[i,j],d[i,k]+d[k,j]);

注意floyd中有时候要用到一个函数memcpy(d,g,sizeof g);//d是dist数组，g是原图，

因为我们跑最短路最好不要在原图上面跑，后面可能会用到原图。

memset(g,0x3f,sizeof g);//初始化
for(int i=1;i<=n;i++) g[i][i]=0;
for(int i=1;i<=m;i++)
{
    int x,y,z;
    cin>>x>>y>>z;
    g[x][y]=g[y][x]=min(g[x][y],z);//防止有重边
}
for(int k=1;k<=n;k++)//floyd
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(g[i][j]>g[i][k]+g[k][j])
                g[i][j]=g[i][k]+g[k][j];

2：传递背包：离散数学i可以到k，k可以到j，呢么i就可以到j。初始化化可以到达的点为1,不能到达的点为0。

3：最小环

我们把环分类，按照环中最大节点的编号分类。 我们开始枚举k的时候，已经求得了任意两点只经过编号为1~k-1的最短路径，这恰好可以帮助我们求环。 环一定是i-k-j这是边，然后j-…-i，这个路径只能包含1~k-1，否则环还可以更短。 所以当k固定的时候，我们只需要枚举i和j（i和j应该都小于k）。 pos[i,j]表示i到j需要经过的中间节点

#include <bits/stdc++.h>
using namespace std;
const int N = 105;
int g[N][N], pos[N][N], d[N][N];
int n, m;
vector<int> v;
void get_pos(int x, int y)//输出x到y之间不包括x和y的道路
{
    if (pos[x][y] == 0) return;//x和y之间没有中间点
    get_pos(x, pos[x][y]);
    v.push_back(pos[x][y]);
    get_pos(pos[x][y], y);
}
int main() {
    cin >> n >> m;
    memset(g, 0x3f, sizeof g);//初始化
    for (int i = 1; i <= n; i++) g[i][i] = 0;
    for (int i = 1; i <= m; i++) {
        int x, y, z;
        cin >> x >> y >> z;
        g[x][y] = g[y][x] = min(g[x][y], z);
    }
    memcpy(d, g, sizeof g);//一个存图，一个跑最短路！！！
    int ans = 1e9;
    //如果存在一个最小环的话，呢么环上的点必定不重复
    for (int k = 1; k <= n; k++) {
        //这里已经求得了从i->j，最大点编号为k-1的最短路
        //我们把环分类，以环中最大点的编号分类,呢么环一定是 i-k-j-...-i，注意i-k-j为两个边，
        //我们枚举i到j就行，所以只要i-j（只经过1~k-1个点）最小就行
        for (int i = 1; i < k; i++)//注意范围
        {
            for (int j = i + 1; j < k; j++)//i和j不相同
            {
                if (ans > (long long) d[i][j] + g[i][k] + g[k][j])//有可能0x3f3f3f3f累加爆int
                {
                    v.clear();
                    ans = d[i][j] + g[i][k] + g[k][j];
                    v.push_back(i);
                    v.push_back(k);
                    v.push_back(j);
                    get_pos(j, i);
                }
            }
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                if (d[i][j] > d[i][k] + d[k][j]) {
                    d[i][j] = d[i][k] + d[k][j];
                    pos[i][j] = k;
                }
            }
        }
    }
    if (ans == 1e9) puts("No solution.");
    else {
        for (auto i: v) {
            cout << i << " ";
        }
    }
    return 0;
}

4：恰好经过k条边的最短路

判负环

（1）由于负环可能并不包含1号点，或者图不连通。所以要建立一个超级源点，从这个点向各个点连一条边权是0的边，然后进行Spfa的第一次出队更新，这等价于初始就将所有点入队。

（2）所以当存在超级源点的时候，求负环时不需要将所有点全部入队了。

（3）求负环或者正环，与dist[i]初始值无关，因为有负环dist就会被不断更新为负无穷，反之为正无穷。但是求最短路顺便判断负环的时候，dist[i]设为正无穷。求最长路顺便判断正环的时候，dist[i]设为负无穷。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 100, M = N;
int h[N], e[M], ne[M], w[M], idx, n, m, st[N], dist[N], cnt[N];
void add(int x, int y, int z) {
    e[idx] = y, w[idx] = z, ne[idx] = h[x], h[x] = idx++;
}
bool spfa() {
    queue<int> q;
    memset(dist, 0x3f, sizeof dist);
    for (int i = 1; i <= n; i++) {
        q.push(i);
        st[i] = 1;
    }
    while (!q.empty()) {
        int t = q.front();
        q.pop();
        st[t] = 0;
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (dist[j] > dist[t] + w[i]) {
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;
                if (cnt[j] >= n) return true;
                if (!st[j]) {
                    st[j] = 1;
                    q.push(j);
                }
            }
        }
    }
    return false;
}
int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int x, y, z;
        cin >> x >> y >> z;
        add(x, y, z);
    }
    if (spfa()) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

差分约束

只要存在一个点可以走到所有点，呢么一定可以走到所有边。

当建立超级源点的边权为0时，等价于将所有点入队。边权不为0还是得建立一个超级源点。

有超级源点了，判断负环不需要将所有点入队，这个超级源点可能是题目中有，或者你自己建立。

如果所有边权都是>=0，并且要求最长路，呢么可以用强连通分量解决，正环等价于强连通分量不存再一条>0的边

最近公共祖先

#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define endl "\n"
typedef long long LL;
const int N = 1e5 + 10, M = 2 * N, mod = 1e9 + 7;
using namespace std;
int h[N], e[M], ne[M], idx, root, n, m;
int f[N][18], depth[N];
void add(int x, int y){
    e[idx] = y, ne[idx] = h[x], h[x] = idx ++;
}
void dfs(int u, int fa){
    for(int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        if(j == fa) continue;
        depth[j] = depth[u] + 1;
        f[j][0] = u;
        for(int k = 1; k <= 17; k ++){
            f[j][k] = f[f[j][k - 1]][k - 1];
        }
        dfs(j, u);
    }
}
int lca(int x, int y){
    if(depth[x] < depth[y]) swap(x, y);
    for(int k = 17; k >= 0; k --){
        if(depth[f[x][k]] >= depth[y]){
            x = f[x][k];
        }
    }
    if(x == y) return x;
    //没有depth了
    for(int k = 17; k >= 0; k --){
        if(f[x][k] != f[y][k]){
            x = f[x][k];
            y = f[y][k];
        }
    }
    return f[x][0];
}
int main()
{
    cin >> n;
    memset(h, -1, sizeof h);
    for(int i = 1; i <= n; i ++){
        int x, y;
        cin >> x >> y;
        if(y == -1) {
            root = x;
            continue;
        }
        add(x, y), add(y, x);
    }
    depth[root] = 1;
    dfs(root, -1);
    cin >> m;
    while(m --){
        int x, y;
        cin >> x >> y;
        int z = lca(x, y);
        if(z == x) cout << 1 << endl;
        else if(z == y) cout << 2 << endl;
        else cout << 0 << endl;
    }
    return 0;
}

树上差分

将a到b路径上的所有边全部+c，可以先d[a]+=c，d[b]+=c , d[lca(a,b)]-=2c;

最后在一遍dfs求出最终的各边权值

以x节点为根，子树的点权值之和就是x节点与之父节点的边权。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 100010, M = 2 * N;
int h[N], e[M], ne[M], idx;
int depth[N], d[N], f[N][18];
int n, m;
LL ans;
void add(int x, int y) {
    e[idx] = y, ne[idx] = h[x], h[x] = idx++;
}
void bfs() {
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0, depth[1] = 1;
    queue<int> q;
    q.push(1);
    while (!q.empty()) {
        int t = q.front();
        q.pop();
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (depth[j] > depth[t] + 1) {
                depth[j] = depth[t] + 1;
                q.push(j);
                f[j][0] = t;
                for (int k = 1; k <= 17; k++) {
                    f[j][k] = f[f[j][k - 1]][k - 1];
                }
            }
        }
    }
}
int lca(int x, int y) {
    if (depth[x] < depth[y]) swap(x, y);
    for (int i = 17; i >= 0; i--) {
        if (depth[f[x][i]] >= depth[y]) {
            x = f[x][i];
        }
    }
    if (x == y) return x;
    for (int i = 17; i >= 0; i--) {
        if (f[x][i] != f[y][i]) {
            x = f[x][i];
            y = f[y][i];
        }
    }
    return f[x][0];
}
int dfs(int x, int fa) {
    LL res = d[x];
    for (int i = h[x]; ~i; i = ne[i]) {
        int j = e[i];
        if (j != fa) {
            res += dfs(j, x);
        }
    }
    if (x == 1) return 0;
    if (res == 0) ans += m;
    else if (res == 1) ans += 1;
    return res;
}
int main() {
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for (int i = 1; i < n; i++) {
        int x, y;
        cin >> x >> y;
        add(x, y), add(y, x);
    }
    bfs();
    for (int i = 1; i <= m; i++) {
        int x, y;
        cin >> x >> y;
        d[x]++, d[y]++, d[lca(x, y)] -= 2;
    }
    dfs(1, -1);
    cout << ans << endl;
    return 0;
}

强连通分量

有向图

时间复杂度线性

强连通分量一定有环，但是不一定就是一个环

环一定是强连通分量

/*
1. 加时间戳；
2. 放入栈中，做好标记；
3. 遍历邻点
    1）如果没遍历过，tarjan一遍，用low[j]更新最小值low
    2) 如果在栈中，用dfn[j]更新最小值low
4.找到最高点
    1）scc个数++
    2）do-while循环：
        从栈中取出每个元素；标志为出栈；
        对元素做好属于哪个scc；该scc中点的数量++
*/
// tarjan 算法求强连通分量
// 时间复杂度O(n+ m)
void tarjan(int u){
    // 初始化自己的时间戳
    dfn[u] = low[u] = ++ timestamp;
    //将该点放入栈中
    stk[++ top] = u, in_stk[u] = true;
    // 遍历和u连通的点
    for(int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        if(!dfn[j]){
            tarjan(j);
            // 更新u所能遍历到的时间戳的最小值
            low[u] = min(low[u], low[j]);
        }
        // 如果当前点在栈中
        //注意栈中存的可能是树中几个不同分支的点,因为有横叉边存在
        // 栈中存的所有点，是还没搜完的点，同时都不是强连通分量的最高点
        // 这里表示当前强连通分量还没有遍历完，即栈中有值
        else if(in_stk[j])
            //更新一下u点所能到的最小的时间戳
            //此时j要么是u的祖先，要么是横叉边的点，时间戳小于u
            low[u] = min(low[u], dfn[j]);
    }
    // 找到该连通分量的最高点
    if(dfn[u] == low[u]){
        int y;
        ++ scc_cnt; // 强连通分量的个数++
        do{// 取出来该连通分量的所有点
            y = stk[top --];
            in_stk[y] = false;
            id[y] = scc_cnt; // 标记点属于哪个连通分量
            size_scc[scc_cnt] ++;
        } while(y != u);
    }
}

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 100, M = 5e4 + 100;
int h[N], e[M], ne[M], idx, n, m;
int timestamp, dfn[N], low[N], scc_size[N], id[N], scc_cnt, dout[N];
bool in_stk[N];
stack<int> stk;
void add(int x, int y) {
    e[idx] = y, ne[idx] = h[x], h[x] = idx++;
}
void tarjan(int u) {
    dfn[u] = low[u] = ++timestamp;
    stk.push(u), in_stk[u] = true;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (!dfn[j]) {
            tarjan(j);
            low[u] = min(low[j], low[u]);
        } else if (in_stk[j]) {
            low[u] = min(low[u], dfn[j]);
        }
    }
    if (dfn[u] == low[u]) {
        int y;
        scc_cnt++;
        do {
            y = stk.top();
            stk.pop();
            in_stk[y] = false;
            id[y] = scc_cnt;
            scc_size[scc_cnt]++;
        } while (y != u);
    }
}
int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int x, y;
        cin >> x >> y;
        add(x, y);
    }
    for (int i = 1; i <= n; i++) {
        if (!dfn[i]) tarjan(i);
    }
    for (int i = 1; i <= n; i++) {
        for (int j = h[i]; ~j; j = ne[j]) {
            int x = id[i], y = id[e[j]];
            if (x != y) {
                dout[x]++;
            }
        }
    }
    int sum = 0, nb;
    for (int i = 1; i <= scc_cnt; i++) {
        if (!dout[i]) {
            sum++;
            nb = i;
        }
    }
    if (sum == 1) cout << scc_size[nb];
    else cout << 0 << endl;
    return 0;
}

缩点

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 100, M = 2e5 + 100;//记得边数翻两倍
int h[N], e[M], ne[M], idx, n, m;
int hh[N];
int dfn[N], low[N], in_stk[N], timestamp, scc_cnt, scc_value[N], a[N], f[N], id[N];
stack<int> s;
void add(int h[], int x, int y) {
    e[idx] = y, ne[idx] = h[x], h[x] = idx++;
}
void tarjan(int u) {
    dfn[u] = low[u] = ++timestamp;
    s.push(u);
    in_stk[u] = 1;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (!dfn[j]) {
            tarjan(j);
            low[u] = min(low[u], low[j]);
        } else if (in_stk[j]) {
            low[u] = min(low[u], dfn[j]);
        }
    }
    if (dfn[u] == low[u]) {
        int y;
        scc_cnt++;
        do {
            y = s.top();
            s.pop();
            in_stk[y] = 0;
            id[y] = scc_cnt;
            scc_value[scc_cnt] += a[y];
        } while (y != u);
    }
}
int main() {
    memset(h, -1, sizeof h);
    memset(hh, -1, sizeof hh);
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= m; i++) {
        int x, y;
        cin >> x >> y;
        add(h, x, y);
    }
    for (int i = 1; i <= n; i++) {
        if (!dfn[i]) tarjan(i);
    }
    for (int i = 1; i <= n; i++) {
        for (int j = h[i]; ~j; j = ne[j]) {
            int x = i, y = e[j];
            if (id[x] != id[y]) {
                add(hh, id[x], id[y]);
            }
        }
    }
    for (int i = 1; i <= scc_cnt; i++) {
        f[i] = scc_value[i];
    }
    for (int i = scc_cnt; i >= 1; i--) {
        for (int j = hh[i]; ~j; j = ne[j]) {
            int k = e[j];
            f[k] = max(f[k], f[i] + scc_value[k]);
        }
    }
    int ans = -0x3f3f3f3f;
    for (int i = 1; i <= scc_cnt; i++) {
        ans = max(ans, f[i]);
    }
    cout << ans << endl;
    return 0;
}

双联通分量

无向图

割边（桥）

边的双连通分量 ： 极大的不包含桥的连通块

边的双连通分量 <=> 任何两个点之间至少存在两个不相交路径

x和y之间是桥 <=> low[y] >dfn[x] y无论如何往上走不到x

将一个图变为边的双联通分量最少要添加几条边：缩点后，（度为1的点的个数+1）/2向下取整

void tarjan(int u, int from)
{
    dfn[u] = low[u] = ++ timestamp;
    stk[ ++ top] = u;
    for (int i = h[u]; i!=-1; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])//j未遍历过
        {
            tarjan(j, i);//dfs(j)
            low[u] = min(low[u], low[j]);//用j更新u
            if (dfn[u] < low[j])//j到不了u
                // 则x-y的边为桥,
                //正向边is_bridge[i] 反向边is_bridge[i ^ 1]都是桥
                is_bridge[i] = is_bridge[i ^ 1] = true;
                // 这里i==idx 如果idx==奇数 则反向边=idx-1 = idx^1
                //            如果idx==偶数 则反向边=idx+1 = idx^1
        }
        // j遍历过 且i不是反向边(即i不是指向u的父节点的边)
        // 因为我们不能用u的父节点的时间戳更新u
        else if (i != (from ^ 1))//不能往回
            low[u] = min(low[u], dfn[j]);
    }
    if (dfn[u] == low[u])
    {
        ++ dcc_cnt;
        int y;
        do {
            y = stk[top -- ];
            id[y] = dcc_cnt;
        } while (y != u);
    }
}

#include <bits/stdc++.h>
using namespace std;
const int N = 5010, M = 20010;
int h[N], e[M], ne[M], idx, n, m;
int dfn[N], low[N], id[N], dcc_cnt, timestamp;
stack<int> stk;
bool is_bridge[M];
int d[N];
void add(int x, int y) {
    e[idx] = y, ne[idx] = h[x], h[x] = idx++;
}
void tarjan(int u, int from)//from表示从哪个边来的
{
    dfn[u] = low[u] = ++timestamp;
    stk.push(u);
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (!dfn[j]) {
            tarjan(j, i);
            low[u] = min(low[u], low[j]);
            if (low[j] > dfn[u]) is_bridge[i] = is_bridge[i ^ 1] = true;//j无论如何也走不到u，说明只有一条路径，是割边（桥）
        } else if (i != (from ^ 1))//肯定不能往回更新，相当于只能往下
        {
            low[u] = min(low[u], dfn[j]);
        }
    }
    if (low[u] == dfn[u]) {
        int y;
        dcc_cnt++;
        do {
            y = stk.top();
            stk.pop();
            id[y] = dcc_cnt;
        } while (y != u);
    }
}
int main() {
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for (int i = 1; i <= m; i++) {
        int x, y;
        cin >> x >> y;
        add(x, y), add(y, x);
    }
    for (int i = 1; i <= n; i++) {
        if (!dfn[i]) tarjan(i, -1);
    }
    for (int i = 0; i < idx; i += 2)//缩点，但是没必要真的缩点，i+=2防止重复计算
    {
        if (is_bridge[i])//i是桥的话
        {
            d[id[e[i]]]++;
            d[id[e[i ^ 1]]]++;
        }
    }
    int sum = 0;
    for (int i = 1; i <= dcc_cnt; i++) {
        if (d[i] == 1) sum++;
    }
    cout << (sum + 1) / 2 << endl;//结论
    return 0;
}

二分图

判断

二分图存在的充分必要条件是没有奇数边的环，二分图一般指的都是无向图

时间复杂度：$O(n+m)$

棋盘问题，很多都是二分图，$(i+j)$为偶数染成1，为奇数染成2

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int h[N], e[N], ne[N], col[N], idx, n, m, x, y;//col中，0表示未染色，1,2表示两种颜色
void add(int x, int y) {
    e[idx] = y;
    ne[idx] = h[x];
    h[x] = idx++;
}
bool dfs(int x, int q)//x表示正在搜索哪个点，q表示要染色的颜色
{

    col[x] = q;//染色
    for (int i = h[x]; i != -1; i = ne[i]) {
        int j = e[i];
        if (col[j] == 0)//如果这个点没被染过色的话
        {
            if (dfs(j, 3 - q) == false) return false;//对这个点染色失败了，就可以返回false
        }//3-q可以让1和2相互转化
        else if (col[j] == q) return false;//这个点已经被染过了，并且颜色和父节点相同
    }
    return true;//不矛盾，染色成功
}
int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    while (m--) {
        scanf("%d%d", &x, &y);
        add(x, y), add(y, x);
    }
    int flag = 0;
    for (int i = 1; i <= n; i++) {
        if (col[i] == 0)//如果这个点没被染过色的话，直接染色
        {
            if (dfs(i, 1) == false)//有一个点染色失败（发生矛盾），就直接可以break
            {
                flag = 1;
                break;
            }
        }
    }
    if (flag == 0) cout << "Yes" << endl;
    else cout << "No" << endl;
}

最大匹配

增广路径，从一个非匹配点出发，依次走非匹配边、匹配边、非匹配边、匹配边，最后走到一份非匹配边的算法

二分图的最大匹配等价于不存在增广路径。

实际复杂的$O(nm)$,但是实际上复杂度远小于$O(nm)$

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;//match放的是女朋友对应的男朋友是谁，bj是为了防止男生重复匹配一个人
int h[N], e[N], ne[N], idx, bj[N], match[N], n1, n2, m, x, y, ans;
void add(int x, int y) {
    e[idx] = y, ne[idx] = h[x], h[x] = idx++;
}
bool find(int x) {
    for (int i = h[x]; i != -1; i = ne[i])//遍历与这名男生相联系的女生
    {
        int j = e[i];
        if (bj[j] == 1) continue;//如果这个女生已经匹配过了，就不在匹配了
        bj[j] = 1;
        if (match[j] == 0 || find(match[j]) == true)//如果女生没有对象，或者女生的对象还可以匹配另一个女生
        {
            match[j] = x;//以这位女生建立关系
            return true;//成功匹配，返回true
        }
    }
    return false;//没有找到对象，返回false
}
int main() {
    cin >> n1 >> n2 >> m;
    memset(h, -1, sizeof h);
    while (m--) {
        scanf("%d%d", &x, &y);
        add(x, y);
    }
    for (int i = 1; i <= n1; i++) {
        memset(bj, 0, sizeof bj);//每一次匹配都要初始化一下
        if (find(i) == true) ans++;//成功匹配答案就加1
    }
    cout << ans;
    return 0;
}

二分图中：

最小点覆盖定义： 二分图中，选出最少的点，使每一条边的两个端点，至少有一个被选中。

最大独立集：二分图中，选出最多的点，使得选出的点之间没有边

最少路径覆盖：用最少的互不相交的路径，将所有点都覆盖住。

最少路径重复的覆盖：

欧拉路径（回路）

欧拉路径：是否存在一种路径，可以使所有的边恰好走一次；

欧拉回路：是否存在一种回路，是所有边恰好走一次并且回到原点

欧拉路径也就是一笔画问题，起点的度必然是奇数，终点的度也是奇数，其他点的度必须是偶数

存在欧拉路径和欧拉回路的前提是所有边联通！！！

无向图存在欧拉路径的充分必要条件：度数为奇数的点只能为2个或者0个（起点=终点）；

无向图存在欧拉回路的充分必要条件：度数为奇数的点只能为0个；

有向图存在欧拉路径的充分必要条件：要么所有点的入度都等于出度（起点=终点）；要么除了两个点外其余的所有点，入度等于出度，这两个点，一个出度比入度多1（起点），另一个入度比出度多1（终点）；

有向图存在欧拉回路的充分必要条件：所有点的入度都等于出度；

数论

质数定理：1~n中质数的个数为$n/ln(n)$

$1~n$中能被$x$整除的个数为$\lfloor$n/x$\rfloor$$下取整

质数

试除法判定质数

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6;
bool f(int x) {
    if (x <= 1) return false;
    for (int i = 2; i <= x / i; i++) {
        if (x % i == 0) return false;
    }
    return true;
}
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        if (f(x)) cout << "Yes" << endl;
        else cout << "No" << endl;
    }
    return 0;
}

埃氏筛

bool st[N];
int primes[N], cnt;
void init(int n) {
    st[0] = st[1] = true;
    for (int i = 2; i <= n; i++) {
        if (!st[i]) {
            primes[cnt++] = i;
            for (int j = i + i; j <= n; j += i) st[j] = true;
        }
    }
}

线性筛法

#include <bits/stdc++.h>
#define endl "\n"
const int N = 1e8 + 10, M = N, mod = 1e9 + 7;
using namespace std;
int primes[N], cnt;
bool st[N];
void init(int n){
    st[0] = st[1] = true;
    for(int i = 2; i <= n; i ++){
        if(!st[i]) primes[++ cnt] = i;
        for(int j = 1; j <= cnt && i * primes[j] <= n; j ++){
            st[i * primes[j]] = true;
            if(i % primes[j] == 0) break;
        }
    }
}
int main()
{
    int n, q;
    cin >> n >> q;
    init(n);
    while(q --){
        int k;
        cin >> k;
        cout << primes[k] << endl;
    }
    return 0;
}

质因数和约数

质因数

#include <bits/stdc++.h>
using namespace std;
void f(int n) {
    for (int i = 2; i <= n / i; i++) {
        if (n % i == 0) {
            int s = 0;
            while (n % i == 0) {
                n = n / i;
                s ++;
            }
            cout << i << " " << s << endl;
        }
    }
    if (n > 1) cout << n << " " << 1 << endl;
}
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        f(x);
        cout << endl;
    }
}

约数

试除法

#include <bits/stdc++.h>
using namespace std;
void f(int x) {
    vector<int> v;
    for (int i = 1; i <= x / i; i++) {
        if (x % i == 0) {
            v.push_back(i);
            if (i != x / i) v.push_back(x / i);
        }
    }
    sort(v.begin(), v.end());
    for(auto it : v) cout << it << " ";
    cout << endl;
}
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        f(x);
    }
    return 0;
}

求约数个数

$N=p_1^{\alpha_1}p_1^{\alpha_2}\cdots*p_1^{\alpha_k}$

$cnt=(\alpha_1+1)(\alpha_2+1)\cdots*(\alpha_k+1)$

#include <bits/stdc++.h>
typedef long long LL;
using namespace std;
const int N = 1e6, mod = 1e9 + 7;
map<int, int> mp;
void solve(int n) {
    for (int i = 2; i <= n / i; i++) {
        while (n % i == 0) {
            n /= i;
            mp[i]++;
        }
    }
    if (n > 1) mp[n]++;
}
int main() {
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        solve(n);
    }
    LL sum = 1;
    for (auto it: mp) {
        sum = sum * (it.second + 1) % mod;
    }
    cout << sum << endl;
    return 0;
}

约数之和

$N=p_1^{\alpha_1}p_1^{\alpha_2}\cdots*p_1^{\alpha_k}$

$sum=(p_1^0+p_1^1+\cdots+p_1^{\alpha_1})\cdots(p_2^0+p_2^1+\cdots+p_2^{\alpha_2})\cdots(p_k^0+p_k^1+\cdots +p_k^{\alpha_k}) $

如何求出$p_k^0+p_k^1+\cdots +p_k^{\alpha_k}$,当成$p$进制，就可以，每一位都是$1*权重$

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e6, mod = 1e9 + 7;
map<int, int> mp;
void solve(int n) {
    for (int i = 2; i <= n / i; i++) {
        while (n % i == 0) {
            n /= i;
            mp[i]++;
        }
    }
    if (n > 1) mp[n]++;
}
int main() {
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        solve(n);
    }
    LL sum = 1;
    for (auto it: mp) {
        LL x = 0;
        for (int i = it.second; i >= 0; i--)//类似于进制转化
        {
            x = (x * it.first + 1) % mod;
        }
        sum = sum * x % mod;
    }
    cout << sum << endl;
    return 0;
}

最大公约数

欧几里得算法: $gcd(a,b)=gcd(b,a%b)$

性质：$ d|a$，$d|b$则 $d|（a+b）$ d能整除a,d能整除b，则d能整除（a+b）很好证明，直接设就行

int gcd(int a, int b) {
    return b ? gcd(b, a % b) : a;
}

扩展欧几里得：求$ax+by=gcd(a,b)$的一组解

通解$x=x_0-b/d*k$ $k$是整数

​ $y=y_0+a/d*k$

x最小非负数是多少？另$t=b/d$ 则 $x=x_0-t*k$

$x_{min}=(x_0\%t+t)\%t$

如何求$ax+by=d$的解？

有解的充分必要条件是$gcd(a,b)|d$

扩展欧几里得求出$ax+by=gcd(a,b)$的一组解，乘上系数即可。

#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 1e6;
int exgcd(int a, int b, int &x, int &y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);//交换一下顺序
    y = y - a / b * x;
    return d;
}
int main() {
    int n;
    scanf("%d", &n);
    while (n--) {
        int a, b, x, y;
        scanf("%d%d", &a, &b);
        int d = exgcd(a, b, x, y);
        printf("%d %d\n", x, y);
    }
    return 0;
}

欧拉函数

$\phi(n)$为$1$~$n$直接中与$n$互质数的个数

快速幂

快速幂求逆元，要求逆元存在（a和p互质），并且p是质数。

LL qpow(LL a, LL b, LL p) {
    LL ans = 1;
    while (b) {
        if (b & 1) ans = ans * a % p;
        b >>= 1;
        a = a * a % p;//这里别忘了mod
    }
    return ans;
}

矩阵快速幂

#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define endl "\n"
typedef long long LL;
const int N = 1e5 + 10, M = N, mod = 1e9 + 7;
using namespace std;
struct Mat{
    LL a[105][105];
    int r, c;
    Mat(int _r, int _c){
        r = _r, c = _c;
        memset(a, 0, sizeof a);
    }
    //单位矩阵
    void unit(){
        memset(a, 0, sizeof a);
        for(int i = 1; i <= r; i ++){
            a[i][i] = 1;
        }
    }
    Mat operator+(const Mat t) const{
        Mat ans = *this;
        for(int i = 1; i <= r; i ++){
            for(int j = 1; j <= c; j ++){
                ans.a[i][j] += t.a[i][j];
            }
        }
        return ans;
    }
    Mat operator-(const Mat t) const{
        Mat ans = *this;
        for(int i = 1; i <= r; i ++){
            for(int j = 1; j <= c; j ++){
                ans.a[i][j] -= t.a[i][j];
            }
        }
        return ans;
    }
    Mat operator*(const Mat t) const{
        Mat ans(r, t.c);
        int n = r, m = t.c;
        for(int i = 1; i <= n; i ++){
            for(int j = 1; j <= m; j ++){
                for(int k = 1; k <= c; k ++){
                    ans.a[i][j] += a[i][k] * t.a[k][j];
                    ans.a[i][j] %= mod;
                }
            }
        }
        return ans;
    }
    Mat pow(LL b){
        Mat ans(r, c), _a = *this;
        ans.unit();
        while(b){
            if(b & 1) ans = ans * _a;
            _a = _a * _a;
            b >>= 1;
        }
        return ans;
    }
    void output(){
        for(int i = 1; i <= r; i ++){
            for(int j = 1; j <= c; j ++){
                cout << a[i][j] << " ";
            }
            cout << endl;
        }
    }
};
int main()
{
    LL n;
    cin >> n;
    Mat a(2, 2), temp(1, 2);
    temp.a[1][1] = temp.a[1][2] = 1,
    a.a[1][1] = 0, a.a[1][2] = a.a[2][1] = a.a[2][2] = 1;
    Mat ans = temp * a.pow(n - 2);
    cout << ans.a[1][2];
    return 0;
}

龟速乘

和快速幂思想一样，快速幂是把乘法变成乘法，龟速乘是把乘法变成加法，速度变慢了，但是不会爆long long

LL qadd(LL a, LL b, LL p) {
    LL ans = 0;
    while (b) {
        if (b & 1) ans = (ans + a) % p;
        b >>= 1;
        a = (a + a) % p;
    }
    return ans;
}

组合数

$C_n^m$ $=$ $n(n-1)(n-2)\cdot\cdot\cdot(n-m+1) \over m(m-1)\cdot\cdot*1$

$C_a^b=$$a!\over b!*(a-b)!$

C[a,b]=C[a-1,b]+C[a-1,b-1];

预处理时间复杂度：$O(N^2)$

const int N = 2005, mod = 1e9 + 7;
int c[N][N];
void init() {
    for (int i = 0; i < N; i++) {
        for (int j = 0; j <= i; j++) {
            if (j == 0) c[i][j] = 1;
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
        }
    }
}

预处理时间复杂度$O(N*log(N))$

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL N = 1e5 + 8, mod = 1e9 + 7;
LL fact[N], infact[N];
LL qmi(LL a, LL k, LL p) {
    LL ans = 1;
    while (k != 0) {
        if (k & 1) ans = ans * a % p;
        k = k >> 1;
        a = a * a % p;
    }
    return ans;
}
void init() {
    fact[0] = infact[0] = 1;//0的阶乘为1，除0的阶乘也为1
    for (int i = 1; i < N; i++) {
        fact[i] = fact[i - 1] * i % mod;
        infact[i] = infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }
}
LL n, a, b;
int main() {
    cin >> n;
    init();
    while (n--) {
        scanf("%lld%lld", &a, &b);
        printf("%lld\n", fact[a] * infact[b] % mod * infact[a - b] % mod);//要及时取模
    }
}

$1<=b<=a<=1e18$

lucas

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int n;
LL qmi(LL a, LL k, LL p) {
    LL ans = 1;
    while (k) {
        if (k & 1) ans = ans * a % p;
        k = k >> 1;
        a = a * a % p;
    }
    return ans;
}
LL p;
LL c(LL a, LL b) {
    if (a < b) return 0;//使用lucas定理有可能a<b
    LL ans = 1;
    LL sum = 1;
    for (int i = 1, j = a; i <= b; i++, j--)//就是高中求组合数的方法
    {
        ans = ans * j % p;
        sum = sum * i % p;
    }
    return ans * qmi(sum, p - 2, p) % p;//为什么可以用快速幂求逆元，因为sum和p一定互质，且p为质数
    //由此可见，p为素数的时候不一定存在逆元，因为不一定互质
}
LL lucas(LL a, LL b) {
    if (a < p && b < p) {
        return c(a, b);//直接用定义求，也是递归的终点
    }
    return c(a % p, b % p) * lucas(a / p, b / p) % p;//一定注意要继续递归，因为a/p可能很大
    //a/p要是大于p的话会出现大麻烦，因为阶乘要mod p
    //a/p=6，p=2的话 a/p%p==0，阶乘怎么可能为0
}
int main() {
    cin >> n;
    while (n--) {
        LL a, b;
        cin >> a >> b >> p;
        cout << lucas(a, b) << endl;
    }
}

容斥原理

时间复杂度$O(2^n)$

分析，有$C_n^1+C_n^3+C_n^2+\cdot\cdot\cdot+C_n^n$，可以补上一个$C_n^0$，所以有$2^n-1$项

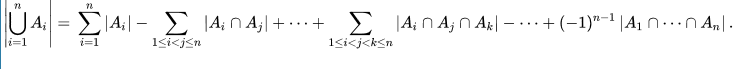
/*容斥原理的应用
能被p1,p2,…,pm 中的至少一个数整除的整数数量
就是p1∪p2∪p3---∪pm，可以由容斥原理算出；
[1,n]中能被x整除的数有[n/x]个；
其中因为p是素数，所以既能被p1整除又能被p2整除的话，
就相当于被p1*p2整除，如何枚举呢？
采用二进制枚举法，需要枚举m个位置，所以从1枚举到pow(2,m-1);不能是从0开始枚举，因为
全是0表示都没选，不符合题意
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 20;
int a[N];
int n, m;
int main() {
    cin >> n >> m;
    for (int i = 0; i < m; i++)//从0开始存的话方便后面二进制枚举
    {
        cin >> a[i];
    }
    LL ans = 0;
    for (int i = 1; i <= pow(2, m) - 1; i++)//枚举所有的方案
    {
        LL sum = 0, t = 1;//sum为奇数符号为+，sum为偶数符号为-
        int flag = 0;//有可能枚举的数的乘积>n,这样不合法,但是最终答案是对的；
        for (int j = 0; j < m; j++) {
            if (i >> j & 1) {
                sum++;
                if (t * a[j] > n) {
                    flag = 1;
                    break;
                }
                t = t * a[j];
            }

        }
        if (flag == 0) {
            if (sum % 2 == 1) ans += n / t;
            else ans -= n / t;
        }
    }
    cout << ans << endl;
}

DP

背包问题

01背包

#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
int dp[N][N], v[N], w[N];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> v[i] >> w[i];//输入物品的体积和价值
    }
    for (int i = 1; i <= n; i++){
        for (int j = 0; j <= m; j++){
            if(j < v[i]) dp[i][j] = dp[i - 1][j];//背包容量不够，选不了
            else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);//决策选还是不选
        }
    }
    cout << dp[n][m];
    return 0;
}

空间优化

#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
int dp[N], v[N], w[N];
int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i++){
        for (int j = m; j >= v[i]; j --){//从大到小枚举，注意j >= v[i]，并且是j --
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    cout << dp[m];
    return 0;
}

求方案数

#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<int,int>PII;
const int N=110;
int f[N][10010];//从前i个里面选，恰好可以表示出来j
int a[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    f[0][0]=1;
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            if(a[i]>j)  f[i][j]=f[i-1][j];
            else f[i][j]=f[i-1][j]+f[i-1][j-a[i]];
        }
    }
    cout<<f[n][m];
    return 0;
}

完全背包

时间复杂度$O(n^2)$

#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
int dp[N][N], v[N], w[N];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> v[i] >> w[i];//输入物品的体积和价值
    }
    for (int i = 1; i <= n; i++){
        for (int j = 0; j <= m; j++){
            if(j < v[i]) dp[i][j] = dp[i - 1][j];//背包容量不够，一个都选不了
            else dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
        }
    }
    cout << dp[n][m];
    return 0;
}

优化版本

#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
int dp[N], v[N], w[N];
int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; i++){
        cin >> v[i] >> w[i];
    }
    for (int i = 1; i <= n; i++){
        for (int j = v[i]; j <= m; j ++){//注意j从v[i]开始枚举
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    cout << dp[m];
    return 0;
}

求方案数

#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int f[2][N], w[N], v[N], n, m;
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= m; j++) {
            if (j < v[i]) f[i & 1][j] = f[(i - 1) & 1][j];
            else f[i & 1][j] = max(f[(i - 1) & 1][j], f[i & 1][j - v[i]] + w[i]);
        }
    }
    cout << f[n & 1][m];
    return 0;
}

多重背包

暴力写法时间复杂度$O(n^3)$

#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n, m;
int v[N], w[N], s[N], f[N][N];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) {
        cin >> v[i] >> w[i] >> s[i];
    }
    for (int i = 1; i <= n; i ++ ){
        for (int j = 0; j <= m; j ++ ){
            for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ ){
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

二进制优化写法 时间复杂度$O(n^2*log(s))$

建议数组开$10*n$

#include <bits/stdc++.h>
using namespace std;
const int N = 12010, M = 2010;//建议N = 10 * n
int n, m, cnt;//cnt是打包后的物品数量
int v[N], w[N], f[M];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ){
        int a, b, s;
        cin >> a >> b >> s;
        int k = 1;
        while (k <= s){
            cnt ++;
            //k个物品进行打包，体积是k*a, 价值是k*b
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        //剩下的就自己打包成一份
        if (s > 0){
            cnt ++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    n = cnt;//新物品的数量是cnt
    //这样就做01背包就行
    for (int i = 1; i <= n; i ++ ){
        for (int j = m; j >= v[i]; j -- ){
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }
    cout << f[m] << endl;
    return 0;
}



#include <bits/stdc++.h>
using namespace std;
const int N = 2010;
int n, m, f[N];
int main()
{
    cin >> n >> m;
    for(int i = 1; i<= n; i ++){
        int a, b, s;
        cin >> a >> b >> s;
        //开始打包
        for(int k = 1; k <= s; k *= 2){
            for(int j = m; j >= k * a; j --){
                f[j] = max(f[j], f[j - k * a] + k * b);
            }
            s -= k;
        }
        //剩下的就自己打包成一份
        if(s){
            for(int j = m; j >= s * a; j --){
                f[j] = max(f[j], f[j - s * a] + s * b);
            }
        }
    }
    cout << f[m];
    return 0;
}

分组背包

时间复杂度$O(n^3)$

#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N][N];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ){
        cin >> s[i];
        for (int j = 0; j < s[i]; j ++ ){
            cin >> v[i][j] >> w[i][j];
        }
    }
    for (int i = 1; i <= n; i ++ ){
        for (int j = m; j >= 0; j -- ){
            f[i][j] = f[i - 1][j];//第i组一个都不选
            for (int k = 0; k < s[i]; k ++ ){
                if (v[i][k] <= j){
                    f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
                }
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

优化空间

#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ){
        cin >> s[i];
        for (int j = 0; j < s[i]; j ++ ){
            cin >> v[i][j] >> w[i][j];
        }
    }
    for (int i = 1; i <= n; i ++ ){
        for (int j = m; j >= 0; j -- ){
            for (int k = 0; k < s[i]; k ++ ){
                if (v[i][k] <= j){
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
                }
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

混合背包

混合背包就是将前面三种的背包问题混合起来，有的只能取一次，有的能取无限次，有的只能取$k$次。

先将01背包和完全背包转化成多重背包。

• 01背包，物品数量为1的多重背包，
• 完全背包，物品数量为$V_{背包体积}/v_i$的多重背包，虽然物品数量是无限的，但是背包容量是有限的。

再按照多重背包来做即可。

#include <bits/stdc++.h>
using namespace std;
const int N = 1005 * 20;
int f[N], w[N], v[N], n, m;
int main()
{
    int cnt = 0;
    cin >> n >> m;
    for (int i = 1; i <= n; i ++)
    {
        int a, b, s;
        cin >> a >> b >> s;
        if (s == 0) s = m / a;//如果是完全背包，则看成多重背包做
        if (s == -1)//01背包
        {
            cnt ++;
            v[cnt] = a, w[cnt] = b;
        }
        else//多重背包二进制拆分
        {
            int k = 1;
            while (k <= s)
            {
                cnt ++;
                v[cnt] = k * a;
                w[cnt] = k * b;
                s -= k;
                k *= 2;
            }
            if (s)
            {
                cnt ++;
                v[cnt] = s * a;
                w[cnt] = s * b;
            }
        }
    }
    for (int i = 1; i <= cnt; i ++)
        for (int j = m; j >= v[i]; j --)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m];
    return 0;
}

思路和代码2

01背包当成数量为1的多重背包，然后进行二进制优化。

完全背包的求法与01背包不同，所以单独算完全背包部分。

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
int f[N];
int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++)
    {
        int v, w, s;
        cin >> v >> w >> s;
        if (!s)//完全背包
        {
            for (int j = v; j <= m; j ++)
                f[j] = max(f[j], f[j - v] + w);
        }
        else
        {
            if (s == -1) s = 1;//01背包当成数量为1的多重背包
            for (int k = 1; k <= s; k *= 2)
            {
                for (int j = m; j >= k * v; j --)
                    f[j] = max(f[j], f[j - k * v] + k * w);
                s -= k;
            }
            if (s)
            {
                for (int j = m; j >= s * v; j --)
                    f[j] = max(f[j], f[j - s * v] + s * w);
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

二维费用背包

#include <iostream>
using namespace std;
const int N = 1010, K = 110;
int n, V, M;
int v[N], m[N], w[N];
int f[K][K];
int main()
{
    cin >> n >> V >> M;
    for (int i = 1; i <= n; ++ i)
        cin >> v[i] >> m[i] >> w[i];
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = V; j >= v[i]; -- j)
        {
            for (int k = M; k >= m[i]; -- k)
            {
                f[j][k] = max(f[j][k], f[j - v[i]][k - m[i]] + w[i]);
            }
        }
    }
    cout << f[V][M] << endl;
    return 0;
}

区间dp

按照区间长度递增枚举，才可以dp

#include <bits/stdc++.h>
using namespace std;
const int N = 505;
int s[N], f[N][N];
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        s[i] = s[i - 1] + x;
    }
    //长度为1都是0
    for (int len = 2; len <= n; len++) {
        for (int i = 1; i + len - 1 <= n; i++)//枚举左端点
        {
            int l = i, r = i + len - 1;
            f[l][r] = 0x3f3f3f3f;//初始化
            for (int k = l; k < r; k++)//分割线
            {
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
            }
        }
    }
    cout << f[1][n];
    return 0;
}

数位dp

数位DP笔记(DFS做法) - AcWing

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6;
int a[30];
int f[30][15];
int dfs(int pos, int pre, int limit, int lead) {
    if (!pos) return 1;//递归终点
    else if (!limit && !lead && f[pos][pre] != -1) return f[pos][pre];//记忆化，只有无限制、无前导零才算，不然都是未搜索完的情况。
    int res = 0, up = limit ? a[pos] : 9;
    for (int i = 0; i <= up; i++) {
        if (abs(i - pre) < 2) continue;
        if (lead && !i) res += dfs(pos - 1, -5, limit && i == up, 1);
        else res += dfs(pos - 1, i, limit && i == up, 0);
    }
    if (!limit && !lead) f[pos][pre] = res;
    return res;
}
int calc(int x) {
    memset(f, -1, sizeof f);
    int len = 0;
    while (x) {
        a[++len] = x % 10;
        x /= 10;
    }
    return dfs(len, -5, 1, 1);
}
int main() {
    int a, b;
    cin >> a >> b;
    cout << calc(b) - calc(a - 1);
    return 0;
}

状态压缩DP

一般要用long long

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 12;
ll n, s, k, f[N][105][1 << 10];//第一层为枚举到了第i层，第二层为恰好拜访国王的数量，第三层为当前的状态，最坏有pow(2,10)
vector<int> state;//合法的状态
vector<int> h[1 << 10];//当前状态可以转移到哪些状态
bool check(int x) {
    for (int i = 0; i < n; i++) {
        if ((x >> i) & 1 && (x >> (i + 1)) & 1)//相邻的1
        {
            return false;
        }
    }
    return true;
}
int count(int x) {
    int res = 0;
    for (int i = 0; i < n; i++) res += (x >> i) & 1;
    return res;
}
int main() {
    cin >> n >> k;
    for (int i = 0; i < (1 << n); i++) {
        if (check(i)) state.push_back(i);
    }
    for (int i = 0; i < state.size(); i++) {
        for (int j = 0; j < state.size(); j++) {
            if ((state[i] & state[j]) == 0 && check(state[i] | state[j])) {
                h[i].push_back(j);
            }
        }
    }
    f[0][0][0] = 1;
    for (int i = 1; i <= n + 1; i++)//为什么枚举到n+1呢，最后算答案的时候要枚举状态
    {
        for (int j = 0; j <= k; j++) {
            for (int a = 0; a < state.size(); a++) {
                for (auto b: h[a]) {
                    int cnt = count(state[b]);
                    if (cnt > j) f[i][j][b] = f[i - 1][j][b];//类似于01背包，当前状态选不选
                    else f[i][j][b] += f[i - 1][j - cnt][a];
                }
            }
        }
    }
    cout << f[n + 1][k][0];//n+1行，最多是k个，第n+1行一个都不选就是最终的答案
    return 0;
}

博弈论

先手必胜状态：存在一种方式让对手变成先手必败状态。

先手必败状态：无论采取哪种方式，留给对手的都是先手必胜状态。

Nim游戏

先手必胜：$a_1\bigoplus a_2 \bigoplus \cdots \bigoplus a_n \neq 0$

先手必败：$a_1\bigoplus a_2 \bigoplus \cdots \bigoplus a_n=0$

证明：https://www.acwing.com/solution/content/14269/

#include<bits/stdc++.h>
using namespace std;
int main() {
    int n;
    cin >> n;
    int ans = 0;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        ans = ans ^ x;
    }
    if (ans) cout << "Yes";
    else cout << "No";
}

台阶-Nim游戏

先手必胜：$a1\bigoplus a_3 \bigoplus \cdots \bigoplus a{2n+1} \neq 0$

先手必败：$a2\bigoplus a_4 \bigoplus \cdots \bigoplus a{2n}=0$

证明：和NIm游戏类似，若奇数台阶异或不为0，我一定可以操作让奇数台阶异或变为0，之后若对手拿奇数台阶，呢么留给我的必然是异或不为0，若对手拿偶数台阶，我把他往下拿的，在往下拿，这样局面不改变。一直进行下去，必然是对手先遇到奇数台阶为0，之后对手怎么拿石子下去，我把他的石子往下拿，这样我必胜。

SG函数

$mex$运算：找到一个集合里面不存在的最小的自然数，比如$mex{1,2,3}=0$

$sg(x)=k$,则由定义地$x$可以走到的点的$sg$一定包含$[0,k-1]$里面的任何数

$sg$函数性质：多个独立局面的$sg$值，等于这些局面$sg$值的异或和

$sg=0$是先手必败状态，它只能走下$sg$不为0的状态。

$sg$不等于0，是先手必胜状态，它可以走向一个$sg$为0（必败状态）

#include<bits/stdc++.h>
using namespace std;
int a[105], f[10005];
int k, n;
int sg(int x) {
    if (~f[x]) return f[x];
    unordered_set<int> s;
    for (int i = 1; i <= k; i++) {
        if (x - a[i] >= 0) s.insert(sg(x - a[i]));
    }
    for (int i = 0;; i++) {
        if (!s.count(i)) return f[x] = i;
    }
}
int main() {
    memset(f, -1, sizeof f);
    cin >> k;
    for (int i = 1; i <= k; i++) cin >> a[i];
    cin >> n;
    int res = 0;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        res ^= sg(x);
    }
    if (res) cout << "Yes";
    else cout << "No";
    return 0;
}