左孩子右兄弟

题目

3422. 左孩子右兄弟 - AcWing题库

对于一棵多叉树，我们可以通过 “左孩子右兄弟” 表示法，将其转化成一棵二叉树。

如果我们认为每个结点的子结点是无序的，那么得到的二叉树可能不唯一。

换句话说，每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。

给定一棵包含 N 个结点的多叉树，结点从 1 至 N 编号，其中 1 号结点是根，每个结点的父结点的编号比自己的编号小。

请你计算其通过 “左孩子右兄弟” 表示法转化成的二叉树，高度最高是多少。

注：只有根结点这一个结点的树高度为 0。

例如如下的多叉树：

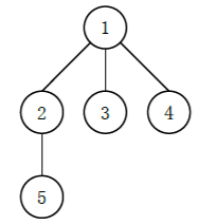
可能有以下 3 种 (这里只列出 3 种，并不是全部) 不同的 “左孩子右兄弟”表示：

其中最后一种高度最高，为 4。

输入格式

输入的第一行包含一个整数 N。

以下 N−1 行，每行包含一个整数，依次表示 2 至 N 号结点的父结点编号。

输出格式

输出一个整数表示答案。

数据范围

对于 30% 的评测用例，$1≤N≤20$；
对于所有评测用例，$1≤N≤10^5$。

输入样例：

5
1
1
1
2

输出样例：

4

思路

这道题思路十分清晰，就是类似于一个递归，已知要把多叉树变成二叉树，显然每个节点只能保留一个子树，那么就变成了保留哪个子树之后二叉树的高度最高，因此可以得出：

最终的高度=保留子树的高度+其兄弟节点的个数

这显然可以用递归解决，记录每个节点的孩子以及孩子的数量。

代码

import java.util.*;

public class Main
{
    final static int N = 100010;
    static int[] E = new int[N];
    static int[] nxt = new int[N];
    static int[] head = new int[N];
    static int[] sum = new int[N];
    static int n, cnt = 0;
    public static void add(int to, int from)
    {
        E[++ cnt] = from;
        nxt[cnt] = head[to];
        head[to] = cnt;
    }
    public static int dfs(int root)
    {
        int ans = 0;
        for(int i = head[root]; i != 0; i = nxt[i])
        {
            ans = Math.max(ans, dfs(E[i]) + sum[root]);
        }
        return ans;
    }
    public static void main(String[] args) {
        Scanner inScanner = new Scanner(System.in);
        n = inScanner.nextInt();
        head[1] = 0;
        nxt[1] = 0;
        for(int i = 2; i <= n; i ++)
        {
            int t = inScanner.nextInt();
            add(t, i);
            sum[t] ++;
        }
        inScanner.close();
        System.out.println(dfs(1));
    }
}
/*
3 3
0 3
1 2
0 2
*/