杨辉三角形

题目

思路：

首先都知道杨辉三角形就是组合数，每一个数都可以被表示出来

如图所示，杨辉三角是左右对称的，所以只用看一半即可

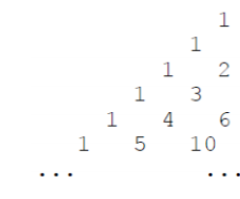
这里我们从右斜着看每一行，也就是

我们可以很明显的从图中发现除了第一行外，每一行都是单调递增的，又因为杨辉三角就是组合数，所以每一行的最小值表示为，$k$是当前行第几个数，如下图所示

因为是斜着的每一行是单调递增的，所以我们可以用二分来找到目标值$n$，又因为每一斜行也是单调递增的，所以我们从最里面开始往外找

上边界就是$l=2k$

下边界就是$r=n$

我们都知道组合数越靠近中间越大，所以由n的范围是$10^9$可以通过计算机算出$\binom{34}{17}>10^9, \binom{32}{16}<10^9$

所以我们可以枚举每一斜行的开头元素(最小元素)$k$,从$16$开始枚举

二分的原理就是如果$C_{mid}^k>=n$,取左区间，否则取右区间。。

当我们找到了这个数的时候即$C_k^r == n$

我们通过规律可以发现$r$为前面共有多少行

第一行$1$个数

第二行$2$个数

第三行$3$个数

…

第$n$行$n$个数

也就是说前面共有$ \frac{r(r+1)}{2}$，$k$为这一行第几个(下标都是从0开始),所以最终的个数是$ \frac{r(r+1)}{2} + k + 1$

代码

import java.util.*;


public class Main {
    static int n;
    public static long C(int m, int k)
    {
        long sum = 1;
        for(int i = m, j = 1; j <= k; i --, j ++)
        {
            sum = sum * i / j;
            if(sum > n)
                return sum;
        }
        return sum;
    }
    public static boolean check(int k)
    {
        int l = 2 *k, r = Math.max(l, n);
        while(l < r)
        {
            int mid = l + r >> 1;
            if(C(mid, k) >= n)
                r = mid;
            else
                l = mid + 1;
        }
        if(C(r, k) != n)
            return false;
        long ans = r;
        System.out.println(ans * (ans + 1) / 2 + k + 1);
        return true;
    }
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        in.close();
        for(int i = 16; i >= 0; i --)
            if(check(i))
                break;

    }
}