双向排序

题目

3419. 双向排序 - AcWing题库

给定序列 $(a_1,a_2,⋅⋅⋅,a_n)=(1,2,⋅⋅⋅,n)$，即 $a_i=i$。

小蓝将对这个序列进行 $m$ 次操作，每次可能是将 $a1,a_2,⋅⋅⋅,a{qi}$ 降序排列，或者将 $a{qi},a{q_i+1},⋅⋅⋅,a_n$ 升序排列。

请求出操作完成后的序列。

输入格式

输入的第一行包含两个整数 $n,m$，分别表示序列的长度和操作次数。

接下来 $m$ 行描述对序列的操作，其中第 $i$ 行包含两个整数 $pi,q_i$ 表示操作类型和参数。当 $p_i$=0 时，表示将 $a_1,a_2,⋅⋅⋅,a{qi}$ 降序排列；当 $p_i$=1 时，表示将 $a{qi},a{q_i+1},⋅⋅⋅,a_n$ 升序排列。

输出格式

输出一行，包含 $n$ 个整数，相邻的整数之间使用一个空格分隔，表示操作完成后的序列。

数据范围
对于 30% 的评测用例，$n,m≤1000$；
对于 60% 的评测用例，$n,m≤5000$；
对于所有评测用例，$1≤n,m≤10^5$，$0≤p_i≤1，1≤q_i≤n$。

输入样例：
3 3
0 3
1 2
0 2
输出样例：
3 1 2

思路：

首先起始的序列是升序的，所以开始的时候是后缀序列是不需要操作的，只有碰到第一个前缀序列是需要操作的，然后可以进行有关的优化

假设蓝色序列为原序列

优化一

如果是多个前缀序列连续或者多个后缀序列连续，可以进行合并。

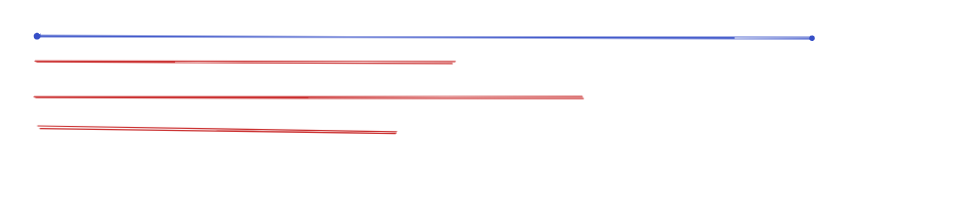
可以选择其中最长的一个前缀序列然后进行操作，同样后缀序列也是如此。

优化二：

前缀序列a，后缀序列b，前缀序列c

前缀序列c的长度$<$前缀序列a的长度

如图所示，对于后缀序列b的A部分的序列是不需要操作的，而对于前缀序列c的C部分的序列也是不需要操作的。

优化三：

前缀序列a，后缀序列b，前缀序列c

前缀序列c的长度$>=$前缀序列a的长度

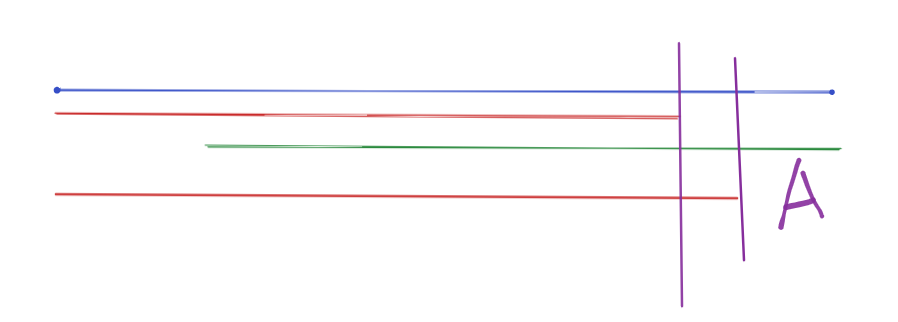
在图中很明显发现A部分不需要任何操作，那么A部分之外的序列，只需要最后一次的前缀操作，即c操作一次降序排序就行了。

以上就是三个小优化，可以通过栈去模拟就行，然后不需要进行排序，进行填充就行。

代码

import java.util.*;

public class Main
{
    static int n, m;
    static node[] a = new node[100010];
    static int[] ans = new int[100010];
    public static void main(String[] args) {
        Scanner inScanner = new Scanner(System.in);
        n = inScanner.nextInt();
        m = inScanner.nextInt();
        int cnt = 0;
        for(int i = 1; i <= m; i ++)
        {
            int op = inScanner.nextInt();
            int p = inScanner.nextInt();
            if(op == 0)
            {
                while(cnt > 0 && a[cnt].x == 0)
                    p = Math.max(p, a[cnt --].v);
                while(cnt >= 2 && a[cnt - 1].v <= p)
                    cnt -= 2;
                ++ cnt;
                //a[++ cnt] = new node(op, p);
            }
            else if(cnt != 0)
            {
                while(cnt > 0 && a[cnt].x == 1)
                    p = Math.min(p, a[cnt --].v);
                while(cnt >= 2 && a[cnt - 1].v >= p)
                    cnt -= 2;
                ++ cnt;
                //a[++ cnt] = new node(op, p);
            }
            a[cnt] = new node(op, p);
        }
        int l = 1, r = n, k = n;
        for(int i = 1; i <= cnt; i ++)
        {
            if(a[i].x == 0)
            {
                while(r > a[i].v && l <= r)
                    ans[r --] = k --;
            }
            else
            {
                while(l < a[i].v && l <= r)
                    ans[l ++] = k --;
            }
            if(l > r) 
                break;
        }
        if(cnt % 2 == 1)
        {
            while(l <= r)
                ans[l ++] = k --;
        }
        else
        {
            while(l <= r)
                ans[r --] = k --;
        }
        inScanner.close();
        for(int i = 1; i <= n; i ++)
            System.out.printf("%d ", ans[i]);
    }
    static class node {
        int x, v;
        public node(int x, int v)
        {
            this.x = x;
            this.v = v;
        }
    }
}
/*
3 3
0 3
1 2
0 2
*/